Tangent Circles and their Loci
by Kristy Hawkins
When exploring tangent circle, I found
it fascinating to look at the locus of the centers of the constructed
tangent circles. Let's look at a few different situations.
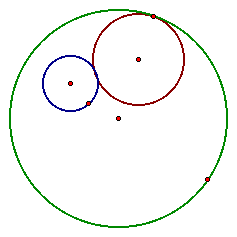
What happens when one of the constructed
circles is inside the other given circle? In tis case, our tangent
circle is inbetween the two given circles and looks much like
this picture where the blue and green circles are given. Click
here for the script of this tangent circle construction.
Now the fascinating part of the exploration.
What happens when we trace the locus of the center of all circles
tangent to the two given circles.
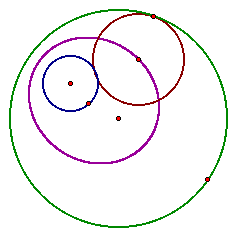It looks like our purple shape is an
ellipse! If you had to make a guess, what would you say the foci
were?
Right, the two foci of the ellipse
are the two centers of our given circle.
Now let's look at a different construction
of a tangent circle. In this picture, the tangent circle is constructed
with the little blue circle on it's inside, and the green circle
on it's ouside, so the picture looks a bit different. Click
here for this script.
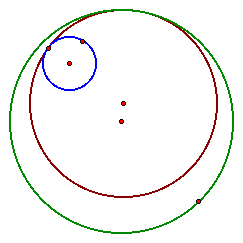What do you think that the locus of
all of the tangent circles will look like in this case? Let's
see!
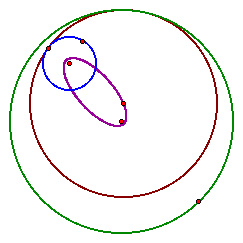We still have an ellipse, but one in
which the foci are much closer to the ellipse itself. But look,
the foci are still the centers of the two given circles. I wonder
if that is true for all of these loci.
Are there anymore cases? Let's look
at what happens when the two given circle are intersecting. That
means our tangent circle will look like this:
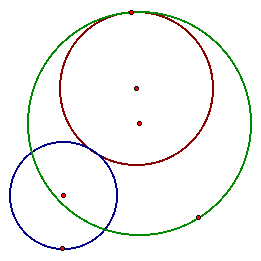This is the first case where the both
of the given circles are on the outside of the tangent circle.
Now let's look at the locus of the centers of all of the tangent
circles. Do you think it will be an ellipse again?
Wow! It is again. The foci of this
ellipse again are the centers of the two given circles. Now let's
look at case two. The tangent circle will look like this picture.
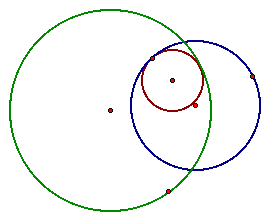Click
here to play with this case and see
where the tangent circle is in relation to each given circle as
it moves around. Did you find anything interesting?
So is the locus of the centers of all
tangent circles going to be an ellipse here?
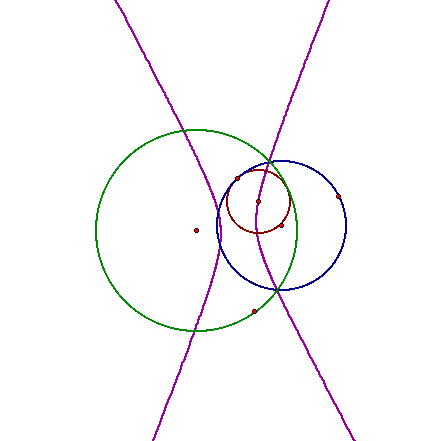That's not an ellipse, it's a hyperbola!
Return