Investigation of Pedal Triangles
by Kristy Hawkins
When we investigate triangles, there is a very interesting
triangle named the Pedal Triangle.
What is the Pedal Triangle?
Let triangle ABC be any triangle. Then if P is any
point in the plane, the triangle formed by constructing the intersections
of the lines through P that are perpendicular to the sides of
our triangle and the segments of triangle ABC is called the pedal
triangle.
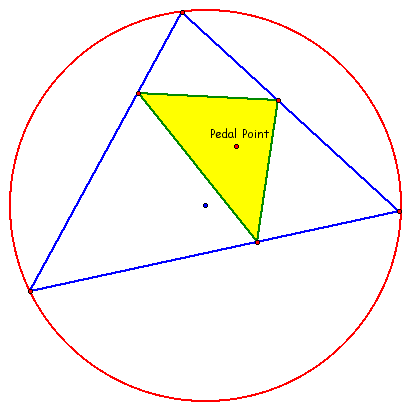Let's investigate this triangle!!
Click here
for a GSP script tool for the pedal triangle.
Since this pedal point can be anywhere, what would
happen if it is at the incenter
of that triangle?
Recall: The incenter of any given triangle is the intersection
point of the angle bisectors. This means that it is equidistant
from all three sides of the triangle and therefore is the center
of the incircle of the triangle.
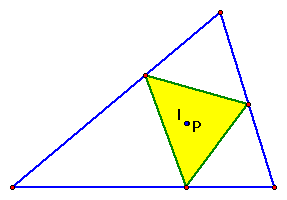Can we find anything interesting about this pedal triangle?
Look at this. If we construct the incircle, it is the
circumcircle of the pedal triangle. Is this true for every triangle?
Click here to play with
the GSP sketch.
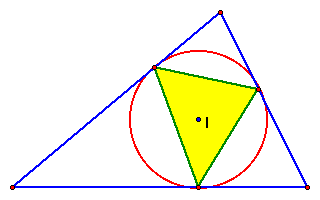Does this make sense? We know that we find the incenter
with the angle bisectors of the original triangle. The radius
of the incircle is then found by dropping a perpendicular line
to one of the sides of the triangle since this is the closest
point from the incenter to the triangle. But that also happens
to be the same point that is a vertex of the pedal triangle.
Since this seems to be true, we can make a conjecture
that when the pedal point of the blue triangle is at it's incenter,
then that same point is also the circumcenter of the pedal triangle.
In other words, the pedal point becomes the circumcenter of the
pedal triangle when it is the incenter of the original triangle.
Wow!
Now what happens when the pedal point is moved to the
circumcenter?
Recall: The circumcenter of a triangle is the point
that lies on the perpendicular bisector of each segment of that
triangle.
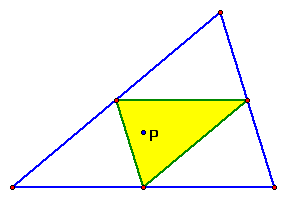This pedal triangle looks familiar! It is the medial
triangle! As the pedal point approaches the circumcenter, the
vertices approach the midpoint of each side of the given triangle
because of the fact that the circumcenter is the intersection
of the perpendicular bisectors of the sides of the triangle. This
medial triangle is similar to the original triangle, and also
one fourth of its area.
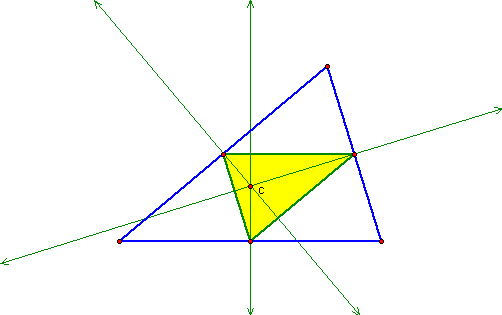If we look at the altitudes of the pedal triangle,
or medial triangle, we see that they look to intersect at our
pedal point which is also the circumcenter of the given triangle.
This would make the pedal point also the orthocenter of the pedal
triangle since the orthocenter is the intersection of the altitudes
of a triangle.
Does anything interesting happen when the pedal point
is moved to the orthocenter?
Recall: The orthocenter of a triangle is found at the
intersection of the three lines that contain the altitudes of
that triangle.
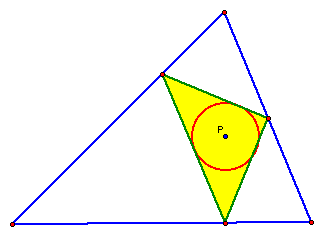The pedal triangle is now the orthic triangle as long
as the original triangle is acute. P also seems to be the incenter
of the pedal triangle while it is the orthocenter of the given
triangle.
Didn't we begin with the pedal point being the incenter
of the given triangle? So we see that the incenter of a given
triangle is the circumcenter of the pedal triangle, the orthocenter
of it's pedal triangle, and the incenter of the pedal triangle
of the pedal triangle of the pedal triangle. That's an interesting
connection. Here is an illustration of it!
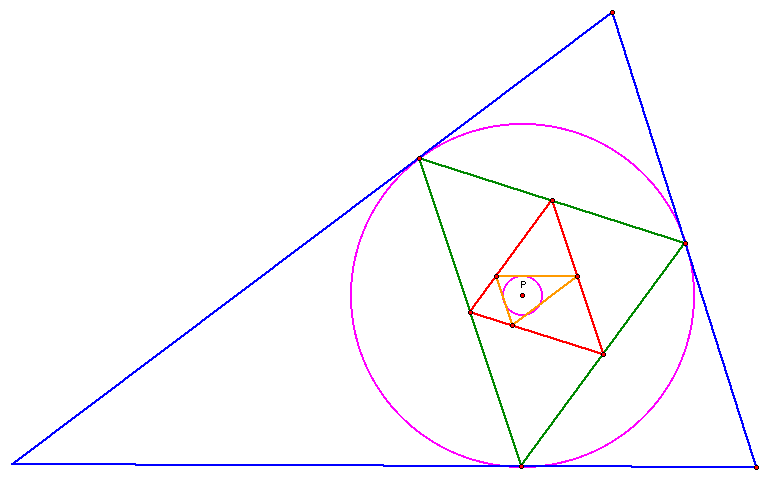In this picture, P is the incenter of the blue triangle,
the circumcenter of the green triangle, the orthocenter of the
red triangle, and then the incenter of the orange triangle. The
bigger pink circle represents the incircle of the blue triangle
as well as the cirrcumcircle of the green triangle. The smaller
pink circle shows the incircle of the orange triangle. This figure
shows us that when the pedal point of the blue triangle is at
it's incenter, it is also at the incenter of the third pedal triangle,
meaning the pedal triangle of the pedal triangle of the pedal
triangle of the original triangle. We can conclude that when P
is in this specific position, it will be the incenter of every
third pedal triangle, the orthocenter of every second pedal triangle,
and the circumcircle of every first pedal triangle. As we continue
the pedal triangles of pedal triangles, the cyclic pattern should
continue forever.
Return