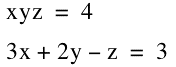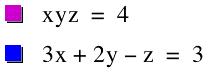Multiple Solutions
by Kristy Hawkins
Find as many solutions as possible for x, y, and z
that satisfy both equations:
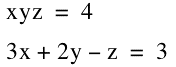Can you think of 3 integers that will satisfy both
of these equations? We can try a guess and check method first.
First of all notice that x, y, and z must all be nonzero because
even if one of them was equal to zero, then xyz=0. So let's try
x=1, y=2. This means that z must equal 2 to satisfy the first
equation. Will this work?
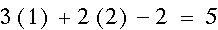Which means that this solution will not work. Instead
of going through this process over and over, let's look at the
two equations graphically.
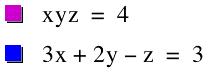
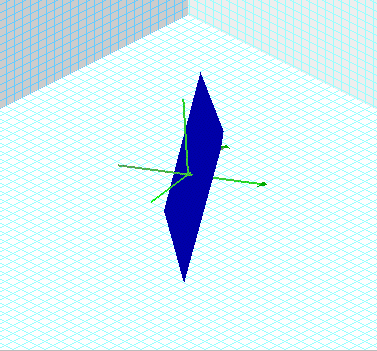Here are the two equations graphed separately in the
three dimensions. The arrows on the green lines indicate the positive
x and y axes. Knowing this will help us determine our solutions.
Now normally when we have two systems of equations in the xy plane,
we would say that the points where they intersect would be their
solutions. The same goes for any 3D equations, so lets see if
we find any solutions when we graph them simultaneously.
At first glance, we notice that one quadrant is left
dry of solutions. From looking at the equations, can you determine
which quadrant this is?
Look at xyz=4. If x, y, and z are all negative, is
there any way that we can get a positive number? Of course not!
So the empty quadrant is the one in which x, y, and z are all
negative.
So we see that there are indeed infinitely many solutions
to these two equations, but how one earth do we find them? One
way that we can begin is by substitution. Let's take our first
equation and solve it for z. Then we can find an equation in terms
of just x and y and graph it on the xy plane.
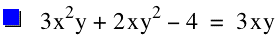
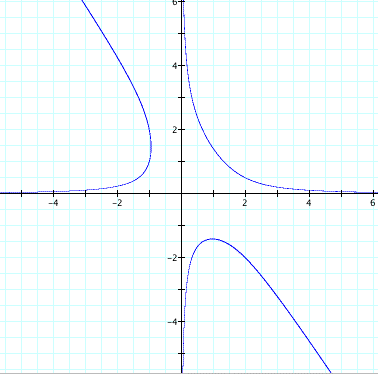This graph looks interesting...what does it tell us
about our solutions? Well, each point on this graph describes
the x and y coordinates of our solution. To find z, we simply
use our equation z=4/(xy). This is a nicer illusration of our
infinite solutions, and notice that we still have not solutions
where x and y are both negative. Can you explain why in your own
words?
Return