Examining Parabolic Curves

 

by

Gloria Jones

 

 

Part I (Graphing Calculator File)

Examine: x(x-4) = y(y-1). What happens if the 4 is replaced by other numbers (not necessarily integers)? Try 5, 3, 2, 1.1, 0.9, (-3). The graph below reflects the original equation in purple and the other new equations. Each equation is color coded to match the curves of the function represented in the graph. Are there any unusual events? Interpret.

 

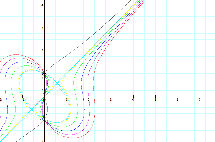
®     x(x-4)=y(y-1)

®     x(x-5)=y(y-1)

®     x(x-3)=y(y-1)

®     x(x-2)=y(y-1)

®     x(x-1)=y(y-1)

®     x(x-1.1)=y(y-1)

®     x(x-0.9)=y(y-1)

®     x(x+3)=y(y-1)

 

Discussion: We start the interpretation with the original equation x(x-4) = y(y-1) in purple. This equation gives a graph of a somewhat symmetrical parabolic shape across the origin. As the (-4) decreases to a larger negative number, the graph seems to hold its shape but expands. See the red graph. Conversely, when (-4) increases to a smaller negative number, the graph is contracted. See (blue, green, and yellow) graphs. Notice how the sky blue graph forms an ellipse with a segment line cutting through the center across the origin. The equation for this shape is x(x-1)=y(y-1). I tried to compare this equation with the ellipse equation, , (a>b) and the line equation y=mx+b. I could not find a direct correlation between the equations. The black graph takes on an asymptotic curve that appears to be perfectly symmetrical across the origin.

 

Part II (Graphing Calculator File)

 

What equation gives the graph below:

 

 

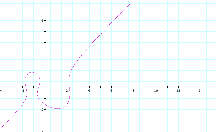
Answer: x(x-4)=y(y-1)+2

 

Part III (Graphing Calculator File)

 

What happens if a constant is added to one side of the equation x(x-4)=y(y-1)? Try several graphs in some systematic way.

 

 

 

 

 

 

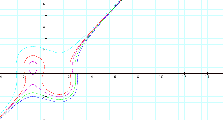
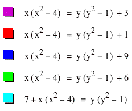
Discussion: Look at what happens when a constant is added to either end of the equation. Of all the constants added in front or in back of the equation, it is the purple graph with equation x(x-4)=y(y-1)+3 that excites me most. As you can see the 3 was added to the back end of the equation forming a graph that has a separate oval-like shape and some parabolic curves. By adding numbers to the back end of the equation, we seem to get more expansive graphs as the number added gets larger. Note that the curve expansion occurs mainly in the I, III, and IV quadrants with the convex region of the graph in the IV quadrant. Conversely, when a constant is added to the front end of the equation, depending on the size of the number, contraction or expansion takes place in the I, II, and III quadrants with the convex region in the II quadrant.

 

 

Part IV (Graphing Calculator File)

 

Try graphing x(x-4)-y(y-1)=z

 

 

 

 

Return