
The Graph of the Parabola
by
Gloria L. Jones
Assignment II
(click here for graphing calc. File)
- Construct graphs for the parabola y=ax²+bx+c for different values of a, b, c. (a, b, c can be any rational numbers). Commonly, y=(x).
Examine: We will explore the quadratic
functions defined by (x)=ax²+bx+c, (a0) and a, b and c are
constants. We will see that the
graph of any quadratic function is a curve called the parabola which is similar or identical in shape to the graph
of y=x². What happens when
a=0? When a=0 the function
becomes a linear equation that forms a line graph as the graph in green.
First, letıs take a look at the original graph in purple of the quadratic equation y=ax²+bx+c where a, b, and c are equal to 1. Notice that the vertex is not centered on the origin. This is because b and c have a value of 1. Now, letıs look at the graph of the basic equation for a parabola y=ax² in blue where the constants b and c are equal to 0. Notice here that the vertex is centered directly on the origin.
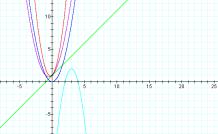
Discussion: From the graphs above in purple, blue, and red, notice that the parabola opens upward. This happens when a>0. From the color key, find that a>0 in each of equations for these graphs. Then look at the graph in light blue where the parabola opens downward. This happens when a<0. For example, the equation for the parabola in light blue is y=(-2)x²+12x-16 where a=(-2) or a<0.
Exploration: We can derive much information from the function of either of the graphs above. Information such the vertex, axis of symmetry, maximum or minimum value of , and x- and y-intercepts can be computed from the equation. Letıs take the function of the graph in light blue and further explore and compute specification of this graph. Recall the function (x)=(-2)x²+12x-16 for the light blue parabola.
- What is the vertex? The vertex is at point (3, 2) found by completing the squares. We get y=-2(x-3)²+2. Other method may be use as well such as calculus. See (Edwards, H., & Penney, D. (2003). Calculus 6e: Early Transcendentals Version.
- What
is the axis of symmetry? The
axis of symmetry is found on the x-axis. It follows that it would be (3) since the (x)
coordinate is (3) for the vertex.
- What
is the maximum value of this function? The max. value in this function is (2). It follows that the max. value
would be (2) since (2) is the (y) coordinate of the vertex.
- What
is the x- and y-intercepts?
First for the x-intercept, we take the equation in #1 and set y to
zero and solve for x. This
gives us 2 and 4. So, we can
see from the graph above that it crosses the x-axis at 2 and 4. For the y-intercept, likewise, set
the x at zero and solve for y.
This gives us (-16) which could have been derived from the original
equation.