
TANGENT CIRCLES
Assignment 7
By
Gloria
L. Jones
The problem in this investigation: Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.
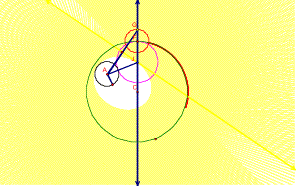
In this assignment we will examine the case: Circle Inside Circle and Point of Tangency on the Interior Circle. Consider the construction below, the center of the desired circle will lie along a line from the center of the given circles with the specified point.

Now we need to locate another locus for the center of the tangent circle. It will look like the following sketch:

Notice the lines through the centers. Now consider the segment from the
center of the desired circle to the center of the second given circle. This segment AJ is always the length of the sum of the radius of the desired circle plus the radius of the given circle.
The same distance can be laid off along the line through the given point from the center of the desired circle by constructing an additional circle of the same radius with center at the designated tangent point:

Now, an isosceles triangle is formed like so:

The center of the desired tangent circle lies along the perpendicular bisector of the base of this isosceles triangle as follows, and now we have a construction of the desired circle:

Click here to trace the center J of all such tangent circles to the two given circles. We notice from the trace that the locus of centers of these tangent circles forms an ellipse with foci at the centers of the two original circles:

If the center of the constructed circle is connected by
segments to the centers of the two given circles, it is immediate that the sum
of the segments is the same as the sum of the radii of the two given
circles. The sum is a constant and
therefore the locus of the centers of the tangent circles is an ellipse with
foci at the centers of the given circles.
Now, when we do a trace of the line as the tangent point of the constructed circle moves around the large circle, an envelope of lines is produced all tangent to the ellipse:
One can explore other possibilities making use of the GSP scripts. Finding the loci of the tangent circle centers that were an ellipse was the only discovery in this problem.
RETURN to Gloriašs Home Page