
POLAR EQUATIONS
Assignment 11
By Gloria L. Jones
In this assignment we will investigate the polar equation r = a+b cos(kθ) for various values of a, b and k. One can click here to view a Graphing Calculator animation of the graphs of r=2+2cos(nθ), r = 3+3 cos(nθ) and r =4+4cos(nθ) for various values (both integer and non integer) of n. At a glance, one notices an overlay of flower (│rose▓) shaped graphs, some with complete leaves and some with partial leaves, some with short leaves and some with longer leaves. Closer analysis yields the following:
Case 1:
r=a+b cos(kθ) where a=b and k is and odd integer.
Looking at the graphs of r=4+4cos θ, r=4+4 cos(3θ) and r=4+4 cos(5θ)
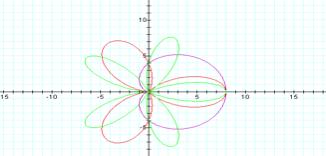
One can deduce rose-shaped graphs with k leaves of length
2a=2b. As k becomes larger, the
leaves appear to grow thinner.
Each leaf appears to be at a 360/kْ rotation from each other
starting from the positive x-axis and all leaves seem to meet at the
origin. The r=4+4 cos θ graph confirms a cardioid shape as
opposed to the multi-leaved rose and all graph appear symmetric with respect to
the x-axis. Looking at the graphs
of r=4+4cos(θ), r=4+4
cos (-3θ) and r=4+4 cos (-5θ),
one detects no change from the previous graphs thus confirming that cos
(-θ) = cosθ.
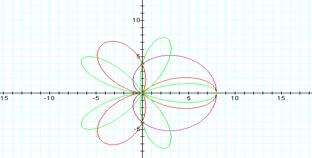
Looking at the graphs of r=2+2 cos
7θ and r=-2-2 cos 7θ one
notices a reflection
over the x-axis which logically follows from r=-2-2cos 7θ = -(2+2cos 7θ).
Case 2: r=
a+b cos (kθ) where a=b and k is an even integer.
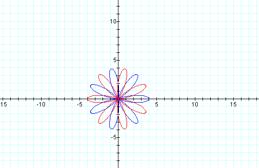
Looking at the graphs of r=4+4
cos (2θ), r=4+4 cos(4θ) and r=4+4 cos (6θ)
one notices many similarities to the odd k graphs: rose-shaped graphs with k leaves of length 2a=2b. As k becomes larger, the leaves become thinner. Each leaf appears to be at a 360/kْ rotation from each other starting from the positive x-axis and all leaves seem to meet at the origin. One difference to notice in the graphs with the even k values is the symmetry with respect to both the x and y axes.
Case 3:
r=a+b cos(kθ) where a=b and k is a non integer
One notices from the graphs of r=4+4 cos(1/2(θ)), r=4+4 cos (4/3(θ) and r=4+4 cos(11/4(θ)) that for non integer values of k, partial leaves occur though further analysis of specific patterns is left for a future investigation.
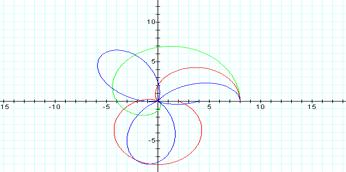
Case 4: r=a+b
cos (kθ) where a>b and k is an odd integer
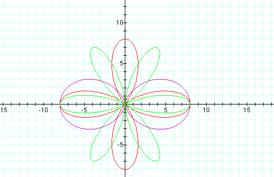
Looking at the graphs of r=3+8
cos (5θ) and r=2+4 cos (5θ) and
r=-3+5 cos (5θ)
one notices similarities to the previous graphs though now smaller leaves appear inside the larger ones. Closer examination reveals the length of the larger leaf to be the larger of b+/-a and the length of the smaller leaf to be the smaller of b+/-a.
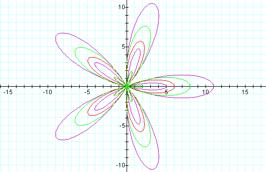
Case 5: r=a+b cos(kθ) where a<b and k is an even
integer
When k is even, one notices the smaller leaves mentioned
above with odd k are now no longer inside the larger leaves but are now between
them: r=3+8
cos (6θ)
Case 6:
r=a+b cos(kθ) where a>b and k is an integer
Looking at the graphs of r=4+2
cos(5θ), r=10+2 cos(5θ) and r=-16+2 cos (5θ)
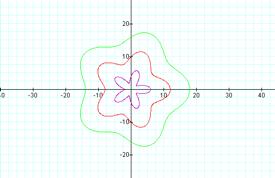
we notice that when a>b, the graphs lose their rose shape though still appear to have k │sections.▓ The sections no longer meet at the origin (and, in fact, the larger the distance between a and b, the further the graph departs from the origin), and the x intercepts appear to be b+/-a.
Assuming a=0 and thus looking at the graphs of r=b cos(kθ), we continue to investigate several cases:
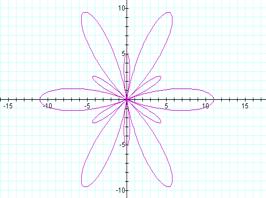
Case 7: r=b
cos(kθ) where k is odd
Looking at the graphs of r=3cosθ,
r=3cos(3θ) and r=3cos(5θ)
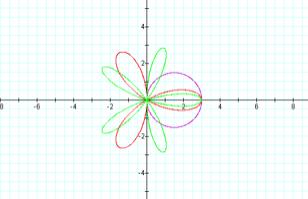
we notice that there are more rose graphs with k leaves but now of length | b| also meeting at the origin and also symmetric with respect to the x-axis.
Case 8: r=b cos(kθ) where k is even
Looking at the graphs of r=4cos(2θ), r=4cos(4θ) and
r=4cos(6θ)
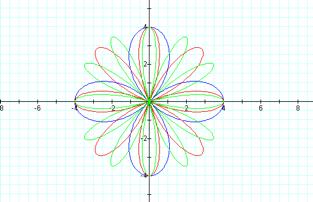
we now notice 2k leaves at a rotation of (360/2k)ْ from each other starting at the positive x-axis and at a length of |b| and symmetric with respect to both the x and the y-axes.
Finally, looking at replacing cos with sin in the previous investigations we notice from the graph of r=4+4 cos(45θ) and r=4+4 sin(45θ) and through many other investigations with Graphing Calc.
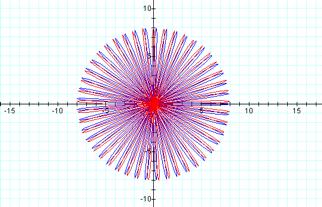
it appears that similar characteristics to the above cases also hold true though the sin graphs appear to have been rotated counterclockwise (90/kْ).