
BOUNCING
BARNEY
Part (A) OF Final
By: Gloria L. Jones
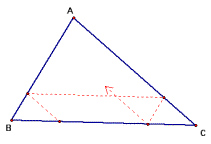
Barney is in the triangular
room. He walks from a point on BC
parallel to AC. When he reaches
AB, he turns and walks parallel to BC.
When he reaches AC, he turns and walks parallel to BC. When he reaches AC, he turns and walks
parallel to AB. Prove that Barney
will eventually return to his starting point. How many times will Barney reach a wall before returning to
his starting point? Explore and
discuss for various starting points on line BC, including points on line
exterior to segment BC. Discuss
and prove any mathematical conjectures you find in the situation.
In this
write-up, we will explore some properties or postulates that will be identified
and useful in proving conjectures in this exploration. Look at the sketch above. Starting at the left point on segment
line BC, Barney will follow the red dashed lines as described above and will
eventually return to where it started.
Barney
accomplishes this return by moving parallel to one of the sides of the triangle
every time it hits a wall. In
moving in this type of pattern, Barney will hit a wall of the triangle five
times before it returns to its starting point. In fact, its path will form a hexagon as shown below:
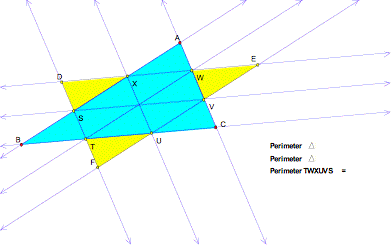
Because
this hexagon was formed by parallel paths cut by yet other parallel lines,
there are some special properties or postulates in this sketch. One of which is when two parallel lines
are cut by a transversal line, then corresponding and alternate interior angles
are equal. The same-side interior
angles are supplementary and the alternate exterior angles are equal. So, in the diagram, we are looking at
six equal triangles in the interior of ΔABC formed by Barneyıs parallel paths.
Notice that
these six triangles are similar triangles to the original triangle. These triangles share the same angle
measurements. Outside of the
hexagon are three triangles in light blue left. These triangles are equal in measurement as those found in
the hexagon. Also, when we
extended the lines beyond the boundaries of the original triangle, more equal
triangles are formed that are similar to ΔDEF. It
should not be a surprise then that the perimeter of ΔABC and the perimeter of TWXUVS are
both equal to 19.92cm. Because of
this phenomenon, Barney will always return to the starting point.
Letıs take
a look at this sketch from the area perspective:
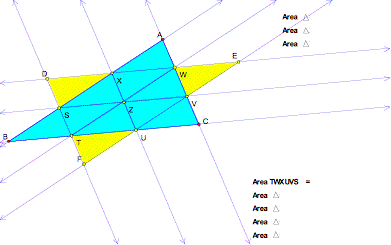
Notice that
the hexagon shaded in light and dark green measure a total of 9.74cm² and
the total area of ΔBAC
is 14.61cm². The ratio
of the hexagon to the total triangle is 2/3 and the three equal triangles
outside of the hexagon measures about 1/3 of the total area. Barneyıs path in dark green makes up
about a third of the total area as well.
Another
method for showing the equality of the perimeters, is measuring the perimeter
of the parallelograms found in the interior of ΔABC compared to the perimeter of ΔABC:
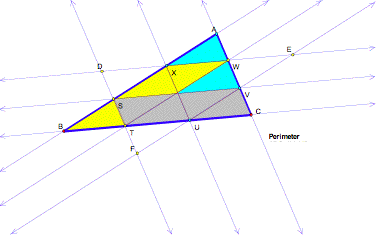
When the
interior triangles are aligned at the centroid, the parallelograms actually span the
entire area of the original triangle.
For each segment on the perimeter of the original triangle, there is a
segment along Barneyıs path with the same length.
Now, letıs
contrast the path of Barney when the starting point is outside of segment BC:
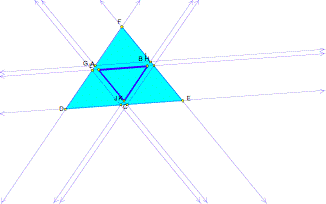
Again we
can see that even starting from a point outside of the segment BC, Barney will
return eventually to its start.
Also as the ΔABC
collapses it appears as if it becomes the area of the path. Nonetheless, because the triangles are
similar, Barney will follow the same path along the segments which will bring
it right back to wherever it started from.
CLICK here to investigate further.