Stamp PRice increase

Final Project Part (C)

By Gloria Jones

3. Consider the Stamp Problem in Assignment 12. Update the data to include the price increases for a first class letter through January 2006 – when the price will become 39 cents. (Recent increases were 33 cents in 1997, 34 cents in 1999, and 37 cents in 2002). Prepare a write-up and use your analysis to answer the questions anew:

-When will the cost of a first class postage stamp reach $1.00?

-When will the cost be 74 cents?

-How soon should we expect the next increase?

In 1996, the analysis of stamp data historically seemed to show that the postage doubled every 10 years approximately. The cost in 2006 would seem to argue that pattern is no longer valid. Is there evidence to show a change in the growth pattern? Or, was the ådoubles every ten yearsπ just a bad model?

Explorations:

In this assignment we start with the observed data given on rates of U.S. postage stamps.

year	rate(in cents)
1919	2
1932	3
1958	4
1963	5
1968	6
1971	8
1974	10
1975	13
1978	15
1981	20
1985	22
1988	25
1991	29
1994	32
1997	33
1999	34
2002	37
2006	39

Next we use the graphics package in Microsoft Excel to better show the function of the curve in terms of increases in the price of stamps over the given years.

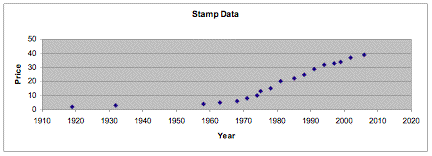
The shape of the plots on the graph above might suggest an exponential function or a power function. We will explore the two options and see which function has the best fit.

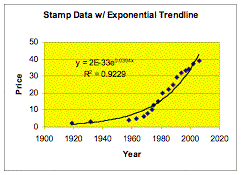
Letπs start with the trend line for the exponential function:

Now look at the trend line for the power function:

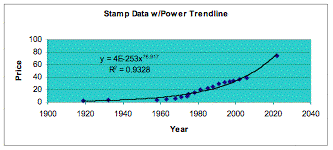
Both graph visually appear to have a pretty close fit but, given their R² value, the power function seem to represent the growth pattern of the stamp rate better. As you can see on the graphs, the exponential R² value is 0.9229 and the power R² value is 0.9328. The power R² is slightly higher than the exponential, giving the best fit.

Using the formulas generated by the chosen functions, we were able to predict approximately the price increases and the date in which the increase would happen:

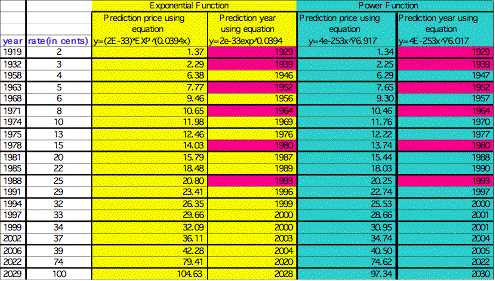
Notice the red highlighted dates are the same for both functions at a given rate. Also notice that the rate at 74 cents was approximated to occur in 2022 and the rate $1.00 in 2029. These years in which the fore mentioned rates occurred were calculated using the growth law formula: N=№e. We were able to solve for t = time.

The exponential function generated the formula y = 2e given the raw data. This formula was used to predict the rate and year in which the rate increase would take place. Notice on the chart above that the predictions are not exact as the raw data. Later we will look at the mean sum of the residual squares to see the variance in the predictions.

The power function generated the formula y = 4x from the raw data. This formula was used in the same manner as the exponential formula to derive at the predictions.

Letπs now look at the chart for the residual year and residual price for the exponential and power functions:

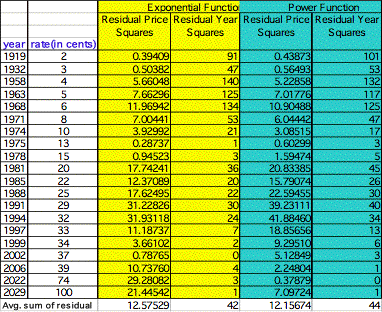
In reviewing the mean sum of the residual values for both functions (price and rate), it appears as either function could be used to predict the growth patterns. As you can see, the exponential function would probably be a better indicator for predicting the year and the power function probably would work better in predicting the price.

In viewing the chart above, historically since 1971, with the exception of years 1975, the rate increase has been every 3 to 4 years. So given that fact, we probably could expect the next rate increase after 2006 to be in 2009 or 2010. Also the data shows that since 1985 the rate has gone up some 2 to 3 cents give some slight exceptions of 1 and 4 cents increase. With that fact alone, over a ten year period, the rate would not have necessarily doubled. I think it is coincidental from 1996 that we see almost a doubling of the rate. It is a poor model to conclude that the rates double every ten years as we can certainly see in 2006 increase.

Return to Gloriaπs Page