
Multiple
Solutions
Final Project Part
B
By Gloria L. Jones
_____________________________________________________________
I). In this write-up we will attempt to
find as many solutions as possible for X, Y, and Z that satisfy both equations:
XYZ = 4
3X + 2Y – Z =
3
Given
the two equations, letıs first observe the possibilities for the
variables.
-We
know that (0) is not a possibility for any of the variables in equation XYZ= 4.
-We
also we know that a system of equation that contains three variables and two
equations provides infinitely many solutions and therefore has no unique
solution. _____________________________________________________________
Using
the Graphics Calculator application, we are able to see graphically the
intersections of the two equations when we substitute Z and solve for X and Y:
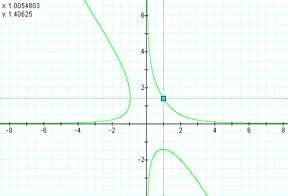
Many
solutions can be obtained from this graphic application by assigning various
values to X to derive the values of Y and Z. Notice on the graph above that the conic curve does not
appear in quadrant III, which might indicate that there is no solution for the
system when all the variables are negative or when there is only one negative
variable. Or that X and Y can not
be negative at the same time.
Letıs look at a chart of possible rounded values:
By
assigning a value for X in the equation XYZ = 4, we are given the value for Y
and by using Microsoft Excel, we are able to obtain the value for Z.
|
X |
Y |
Z |
|
1 |
1.40 |
2.86 |
|
2 |
0.50 |
4.00 |
|
3 |
0.20 |
6.67 |
|
4 |
0.10 |
10.00 |
|
5 |
0.06 |
13.33 |
|
6 |
0.04 |
16.67 |
|
8 |
0.02 |
25.00 |
|
-1 |
1.00 |
-4.00 |
|
-2 |
0.23 |
-8.70 |
|
-3 |
0.11 |
-12.12 |
|
-4 |
0.07 |
-14.93 |
|
-5 |
0.04 |
-18.18 |
|
-6 |
0.03 |
-22.22 |
|
-7 |
0.02 |
-28.57 |
|
-8 |
0.01 |
-50.00 |
This
list of possible solutions to the system of equation could perhaps go on and
on. The asymptotes on the
coordinate plane above suggest that the curves are limited between 10-11
depending on the axes???????
Another observation from a 3 dimensional
view would look like this:

Our
equation 3X + 2Y – Z= 3 is the plane in the graph and equation XYZ =4 is
a conic surface. Where the
two surfaces intersect is where there are solutions. Notice once again that in quadrant III there is no
intersection.
Now
for a view of the equation XYZ = 4 where Z is substituted from equation 3X+
2Y– Z =3, we get XY(3X +2Y -3) =4 in 3 dimension:
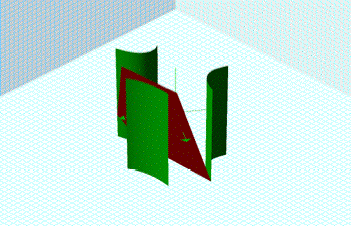
Once
again there is no intersection between the conic surface and the plane in
quadrant III. In fact, it appears
an intersection only takes place in quadrant IV. Which might indicate that when X is positive, Y and Z are
positive and when X is negative, Y is positive and Z is negative.
II). Take a moment and try to explore the
following system of equations for solutions to XYZ using Graphics Calculator
and Microsoft Excel:
2X² +XY +Z= 15
XYZ= 20
Good
Luck!!!