Begin with any quadratic function you like.
I will use
f(x) = x2 + x - 6
Take a look at the graph of your function:
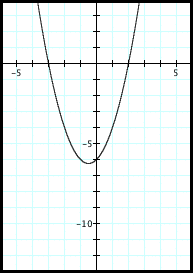
y = f(x)
Now predict what would happen if you replaced
each x in your function with (x-2).
Will the graph change shape? Position? Both?
.gif)
 y = f(x-2)
y = f(x-2)
 y = f(x)
y = f(x)
Is this what you predicted?
You might have thought the graph would move in the negative-x direction, since we subtracted 2 from each of the x's.
So why isn't this what happened?
Imagine you're graphing f(x-2) by hand.
At x = 0, you have to say to yourself, "What is f(x-2)?"
To find out, you can use your original graph (y = f(x))
to find the y-value at x = 0-2 = -2.
Then you have to "drag" this point back to the right
on your new graph to plot it at x = 0.
A graph is made up of infinitely many points, each of which
you have to drag to the right to make the graph of f(x-2).
This is why the graph has shifted to the right
(that is, in the positive-x direction).
Try graphing f(x-a) for various values of a.
You can use this Graphing Calculator file if you like.
What do you see? What happens when a < 0? a > 0?
Does the same pattern hold for non-quadratic functions?
Last time, we replaced every x with (x-2).
What if we replaced every x with (2x)?
Make a prediction, then graph f(2x).
.gif)
 y = f(2x)
y = f(2x)
 y = f(x)
y = f(x)
Again, you might not have expected this.
We multiplied x by 2, but the graph actually got "squished" horizontally. Why?
Once again, think about what you have to do to graph f(2x).
To graph the point (3,f(2·3)), you need to determine f(2·3)
and then drag it back to x = 3.
So you're taking points and dragging them back to points whose
x-coordinate is half as far from the origin.
This is why the graph is getting "squished."
Try graphing f(ax) for various values of a.
You can use this Graphing Calculator file if you like.
What happens if a < 0? |a| < 1? |a| > 1?
What happens as a approaches 0?
Does the same pattern hold for non-quadratic functions?
So far we've worked "inside the parentheses," graphing f(x-2) and f(2x).
What if we did something "outside the parentheses"?
Predict what the graph of f(x) - 2 would look like, then graph it.
-2.gif)
 y = f(x) - 2
y = f(x) - 2
 y = f(x)
y = f(x)
This time the graph moved vertically, and in the negative-y direction.
Wait a second! When we worked inside the parentheses, subtracting 2 moved the graph in the positive-x direction. Why the difference?
Think about how you would graph f(x) - 2
versus how you would graph f(x-2).
To graph f(x-2), we have seen that you have to "grab" points from the y = f(x) graph and drag them back to where you want them,
so the graph moves in the opposite direction of what you might expect.
To graph f(x) - 2, though, you just need to find the point (x,f(x))
and subtract 2 from the y-coordinate.
That is, you just need to move your point downward by 2 units.
There's no weird "dragging back" going on.
Try graphing f(x) - a for various values of a.
You can use this Graphing Calculator file if you like.
What do you see? What happens when a < 0? a > 0?
Does the same pattern hold for non-quadratic functions?
Finally, let's look at graphs of the form a·f(x).
Predict what the graph of 2·f(x) would look like, then graph it.
.gif)
 y = 2·f(x)
y = 2·f(x)
 y = f(x)
y = f(x)
This time the graph got stretched vertically.
Why?
To graph y = 2·f(x), you need to find the point (x,f(x)) and then multiply the y-coordinate by 2.
Again, there's no weird "dragging back" that you have to do; you're just making each point twice as far from the y-axis.
Try graphing a·f(x) for various values of a.
You can use this Graphing Calculator file if you like.
What happens if a < 0? |a| < 1? |a| > 1?
What happens as a approaches 0?
Does the same pattern hold for non-quadratic equations?
Here's an interesting question:
It seems like we could describe the graph of 2f(x) as
being stretched vertically or squished horizontally,
so it seems like we should be able to describe 2f(x) as
f(a·x) for some constant a.
Is this really true?
The answer lies in the roots of the equation.
Look at the roots of f(x) and 2f(x).
They're the same!
But then look at the roots of f(x) and af(x).
They're different whenever a ≠ 1.
So we cannot describe 2f(x) as f(a·x) for any value of a.
That is, horizontal "squishes" and vertical stretches aren't really the same thing, at least for quadratic functions.
Can you find a type of function for which any vertical stretch a·f(x)
can also be described as a horizontal "squish" f(b·x) for some b?
Return to my page
Return to EMAT 6680 page


.gif)
 y = f(x-2)
y = f(x-2)
 y = f(x)
y = f(x)
.gif)
-2.gif)
.gif)