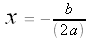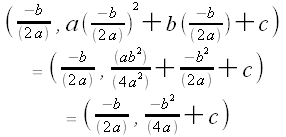Quadratic Functions
|
|
Consider the quadratic function
f(x) = ax2 + bx + c
The graph of this function is a parabola. What effect does changing the values of a, b, or c (while holding the other two constant) have on the vertex of the parabola? Let's find out!
First, we need to know the coordinates of our parabola's vertex. We can see that the vertex lies on the axis of symmetry:
Let's find the equation for the axis of symmetry
First, we complete the square:
This corresponds to taking the parabola described by y = x2 and applying a horizontal shift The axis of symmetry of the parabola described by y = x2 is the line x = 0 (since (-x)2 = x2).
The stretch and vertical shift do not affect the axis of symmetry;
Thus, the vertex of the parabola lies at
Now let's see what happens when we change a, b, or c. Click here to continue.
|
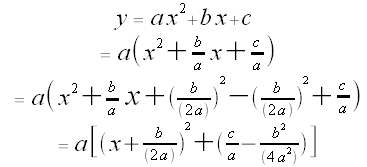
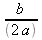 units to the left, a vertical shift
units to the left, a vertical shift 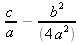 units up, and then a vertical stretch by a factor of
units up, and then a vertical stretch by a factor of 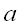 .
.