
Parabola Construction
|
||||||||||
|
A parabola consists of all points which are equidistant from a line d (the directrix) and a point F (the focus), where the focus does not lie on the directrix. Given a directrix and a focus, let's construct a point which lies on the parabola.
Given any point X on d, I claim that the following construction generates a point P which is equidistant from F and d:
In GSP, if I animate X and trace the point P, I will trace a parabola. Click here for the GSP file.
Now I will prove that the point P is equidistant from d and F.
The distance from P to d is the length of the segment which is perpendicular to d and whose endpoints are P and some point on d. That is, the distance from P to d is precisely the length of
And the distance from P to F is simply the length of
So I need to show that
h is the perpendicular bisector of
Also, since h is a perpendicular bisector, we must have
And
So, by the SAS congruence postulate, we have
Thus, Therefore, P is equidistant from d and P. Q.E.D.
We can use this construction to determine the equation describing a parabola with focus (a, b) and a horizontal directrix described by y = y0. Click here to see how.
|
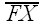 .
.
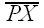 .
.
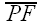 .
.
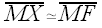 .
.
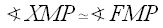 .
.
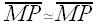 , clearly.
, clearly.
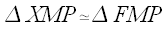 .
.
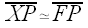 , and so their lengths are equal.
, and so their lengths are equal.