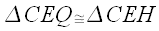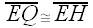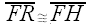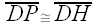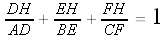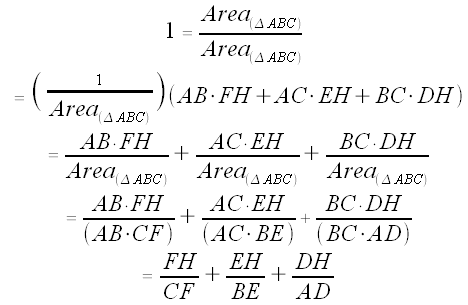Altitudes and Circumcircles
|
|
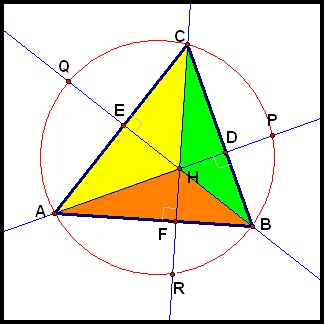
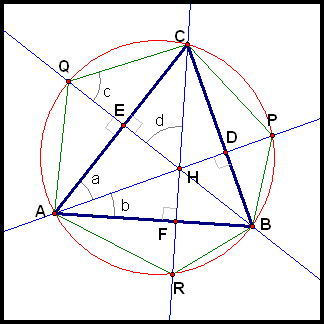
Let ΔABC be any acute triangle, and label it as follows (see below for a diagram): Draw the three altitudes of ΔABC, and let D, E, and F be the intersections of these altitudes with the side of the triangle to which they are perpendicular. Finally, let P, Q, and R be the intersections of the altitudes with the circumcircle (other than A, B, and C).
Using this GSP file, make a conjecture about the following sum:
Can you find any pairs of congruent segments?
It looks like Let's prove it!
First, let's modify the sum a little bit.
So if we want to show that Let's try the second one.
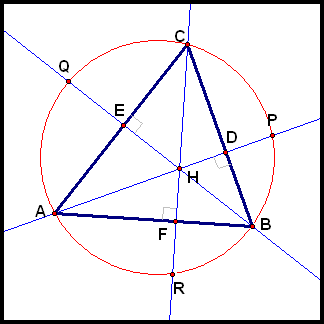
Draw in hexagon CPBRAQ and label some angles as shown:
We know that two angles on a single circle which subtend the same segment are congruent (see Assignment 9 for a "proof").
Thus, c = a + b. (1)
Since
Furthermore, since
By (1) and (2), we have
d = a + b = c
Also,
And finally,
So by AAS congruence, we have
Thus,
By similar reasoning, we have
Because of the congruences we just found, we can rewrite (*) as:
Let's look at a few areas.
For the whole triangle, ΔABC, we have
Now let's break the area up into three pieces:
We now have:
So we have
This is precisely what we wanted to show (see (**))! Q.E.D.
|
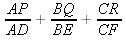
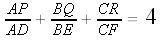

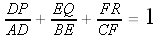
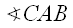 and
and 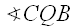 both subtend segment
both subtend segment 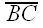 , so they must be congruent.
, so they must be congruent.
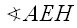 and
and 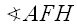 are both right,
are both right,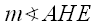 = 90° - a and
= 90° - a and 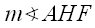 = 90° - b
= 90° - b
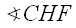 is a straight angle, we have
is a straight angle, we have
 d + 180° - a - b = 180°
d + 180° - a - b = 180°
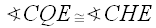
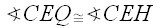 , since both are right angles.
, since both are right angles.
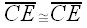 , clearly.
, clearly.