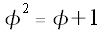φ and Fibonacci
|
|
Mathematicians have long been fascinated by a particular number, called the Golden Ratio. For an excellent read about the properties and surprises of the Golden Ratio, pick up a copy of this book by Mario Livio. There are a lot of equivalent ways to define the golden ratio; let's use the following definition:
For any segment AB, there is a unique point C on AB such that
Let's find the value of
Let x be the length of
By the quadratic formula, we get:
Note that both AC and BC have positive lengths (of course), so
But
We have found two properties of Click here to continue.
|
.
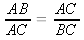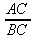(or the equivalent ratio 
)
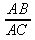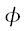, the Golden Ratio.
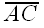, and let y be the length of 
.
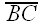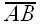is x + y, so
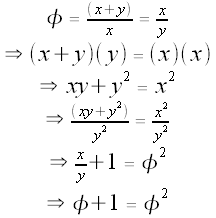
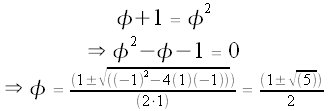
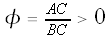
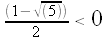, so we must have
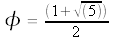
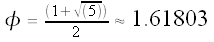and 