
Bouncing Barney
|
|
Imagine a man, Barney, inside a triangular room as below:
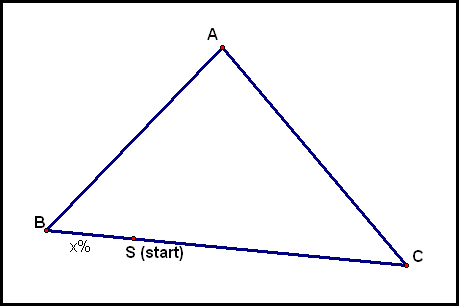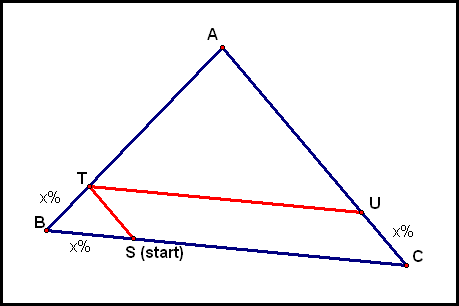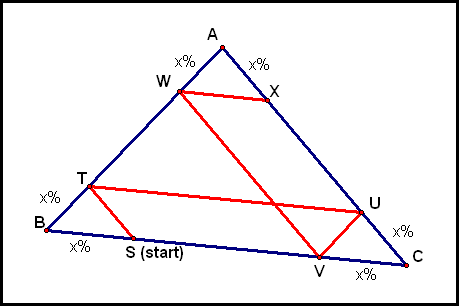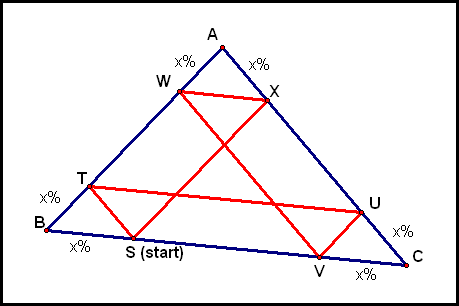
He starts at any point S on wall
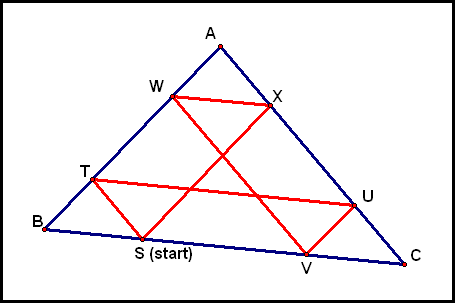
When he hits the wall, he "bounces" off and walks toward wall This pattern continues, and he eventually walks in a path like the one shown below:
Play around with this GSP file for a few minutes and make some observations.
It looks like Barney always returns to his starting point S,
Let's prove it! First, let's prove a general fact about triangles.
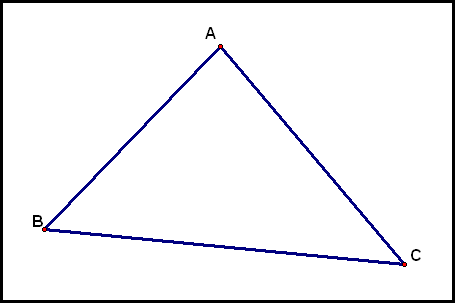
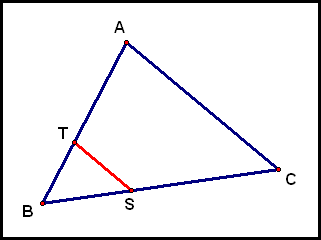
Given triangle ΔABC and points S and T on
You can play around with this GSP file to see if you believe this claim. Now, we'll prove it:
So ΔTBS is similar to ΔABC, by Angle-Angle Similarity. Thus,
Q.E.D.
So, using "x%" along a segment to indicate that that segment is x% as long as the segment of which it is a subset (e.g., BS is x% of BC),
Note that the path Barney walks after bouncing off point X must intersect wall BC at a point Y such that That point is S!
So Barney does indeed return to where he began,
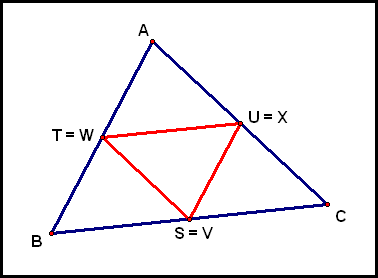
What else did you observe when you were experimenting with the GSP file? One of the things I noticed was that there was a place that I could tell Barney to start bouncing such that he returned to his starting point after only two bounces, instead of five as above.
From the reasoning that went into the animation above, we know that
So S = V must be at the midpoint of
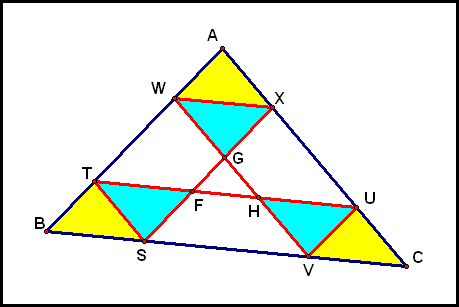
If we label the points at which Barney's path intersects itself as
Looking back at the animation above, we see that the yellow triangles are each similar to ΔABC, and that each of them is "scaled down" to be x% as large as ΔABC. Thus, the yellow triangles are congruent. What about the blue triangles?
Since
And Similarly, because quadrilaterals AXGW and UCVH are parallelograms, we have that all the yellow triangles are congruent to the blue triangles. Thus, the blue triangles are all congruent to each other as well!
It looks like there's a certain spot I can tell Barney to start
We know the following:
(1)
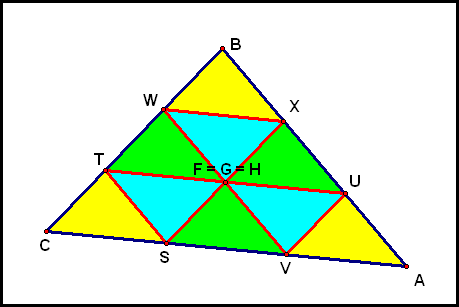
(1) and (2) tell us Since we know the blue and yellow triangles are congruent, this new information tells us that ΔTWF is congruent to those triangles as well! Similarly, ΔFXU and ΔSFV are congruent to those triangles. So the yellow, blue, and green triangles below are all congruent!
So when we are in the case that F = G = H, we have divided ΔABC into 9 congruent triangles. Where does S have to be in order to end up in this case?
We know the yellow and green triangles are congruent, and that
Thus,
So S should be placed at a trisector of
|
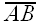 and walks toward wall
and walks toward wall 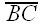 ,
,
 .
.
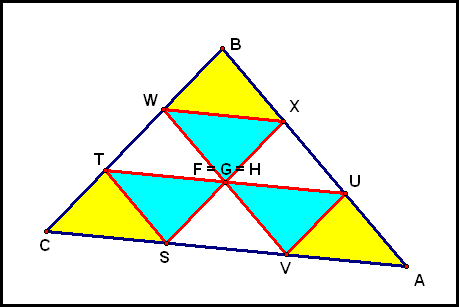
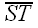 ||
|| 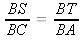 .
.
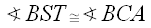 and
and 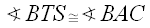 .
.

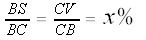 , so if S = V, then we must have
, so if S = V, then we must have
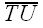 ||
|| 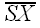 ||
|| 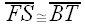 and
and 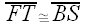
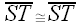 , obviously, so
, obviously, so
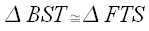
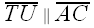
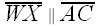
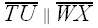 ,
,
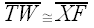 .
.
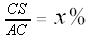 .
.
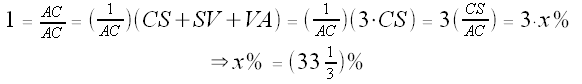 .
.