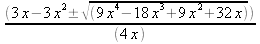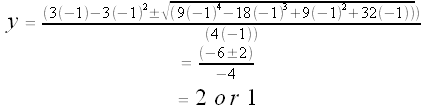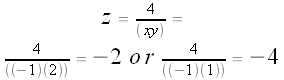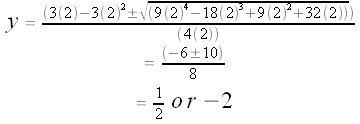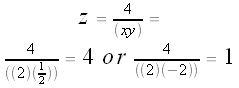Multiple Solutions
|
|
We have been given two equations:
xyz = 4
and we want to find as many solutions to this system of equations as we can. We could proceed using simple guess and check. We know x, y, and z must all be nonzero, since xyz ≠ 0. So that limits our search (although only slightly). Let's try x = y = 2. We want xyz = 4, so we must have z = 1. Does the point (2,2,1) solve the second equation? Let's see. 3(2) + 2(2) - 1 = 9 ≠ 3 So (2,2,1) is not a solution of the system. So let's try x = -1, y = 2. We want xyz = 4, so we must have z = -2. Does the point (-1,2,-2) solve the second equation? 3(-1) + 2(2) - (-2) = 3, as desired. So (-1,2,-2) is a solution of the system. We could continue this process, but it seems pretty slow going. Also, there might be a lot of solutions, and using this process we can never be sure we've found them all. So let's try a new strategy.
Imagine we had been given two two-dimensional equations, like
2x - y = 1
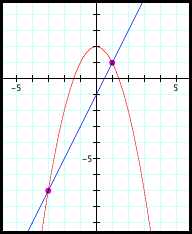
One method of finding solutions is to graph both equations and find their points of intersection:
The solutions to the system are the points of intersection, (-3,-7) and (1,1). We can use a similar strategy to determine some solutions to our three-dimensional equations. There are a couple of differences, though. First, since the equations are three-dimensional, we will need to graph them in x-y-z space, rather than in the x-y plane. Also, since we have three unknowns but only two equations, we will either get an infinite set of solutions, or none at all. Of course, we have already seen that (-1,2,-2) is a solution, so we have at least some solutions. Let's graph our two equations:
The two surfaces do indeed intersect, and, as with the two-dimensional equations, every point in their intersection is a solution to the system. Let's try to determine a description of the intersection. Note that it is a curve, rather than discrete points. We know 3x + 2y - z = 3, so z = 3x + 2y - 3.
So we can substitute this for z into xyz = 4, and we have
Now we can use the Quadratic Formula to solve for y in terms of x:
So our solutions are of the form (x0, y0, z0), where
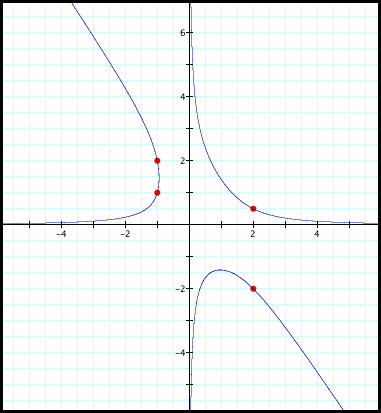
If we project this onto the x-y plane (by setting z = 0), we have the following graph of the x- and y-values of all solutions:
Let's use this information to find some integral solutions to the system.
For our solution to be integral, we need
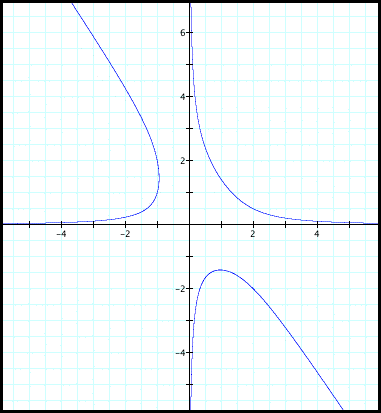
Using a similar strategy as what we used in the two-dimensional example (above), we can graph y = 9x4 - 18x3 + 9x2 + 32x and determine its points of intersection with y = 1, y = 4, y = 9, y = 16, etc. I used my TI-83 and checked y = n2 up to n = 10, and I found that the graph intersects y = 1, y = 9, y = 16, y = 25, y = 36, y = 49, y = 64, and y = 81 at points with irrational x-coordinates. So these will not give us integral solutions to the system.
However, the graph intersects y = 4 at (-1,4),
So x = -1 and x = 2 will give us rational (possibly integral) solutions. Let's determine what those solutions are and see if they're truly integral.
x = -1
x = 2
Note that (-1,2,-2) is the solution we found using guess-and-check (above). But now we've found two more integral solutions:
(-1,2), (-1,1), (2,-2), and (2,0.5) are all points on our projected solution curve:
You can use this Graphing Calculator file to try to locate more points on the projected solution curve. Then you can easily determine the z-coordinate of the solution by finding z = 4 / (xy).
|

 xyz = 4
xyz = 4
 3x + 2y - z = 3
3x + 2y - z = 3
 3x2y + 2xy2 - 3xy - 4 = 0
3x2y + 2xy2 - 3xy - 4 = 0
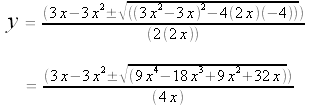
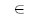 R
R