Oktay Mercimek, EMAT 6690

Bisectors Problem in 120 degree Obtuse Triangle

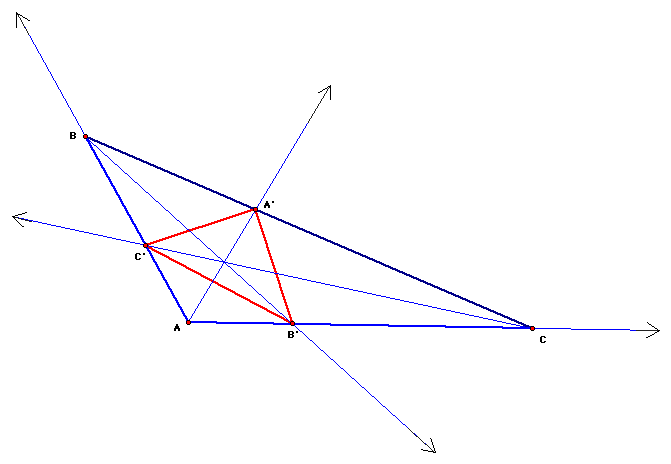
THE PROBLEM:

Let angle A of triangle ABC have measure 120 degrees.


Let A' be the point of intersection of segment BC and the angle
bisector of angle A.
Likewise B' is the intersection of AC and the angle bisector of angle
B, and C' is the intersection of AB and the angle bisector of angle C.

Prove angle B'A'C' is always a right angle.

In order to prove angle B'A'C' is always a right angle, I will use 2 theorems

Theorem 1:

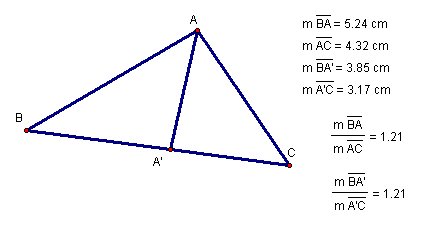AA' is anle bisector. GSP file for the Theorem 1.

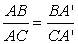if and only if  AA' is angle bisector.

Theorem 2:

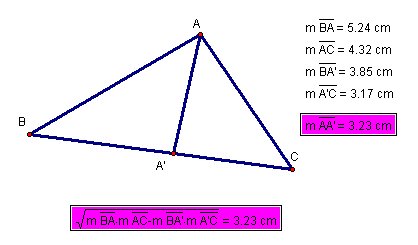
If AA' is angle bisector then AA'=. Click HERE for Proof

Now I can start to solve the problem.

 First we need to determine the lengths of the sides using theorem 1.

AngBis3.gsp

We can label BA' as AB.k and A'C as AC.k  (*1) because it doesn't change the ratio AB/AC. Then using theorem 1 again for AB' , B'C , AC' and C'B, we have

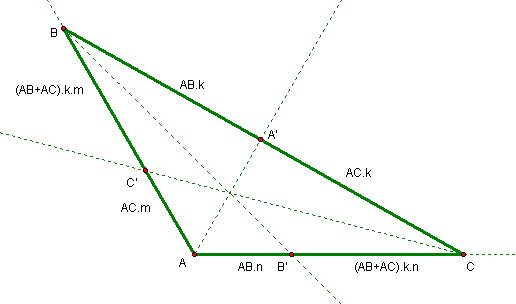
Since Angle BAC is 120 degrees, Angle BAD is 60 degrees. When we drop a perpendicular line to AD from point B, Triangle BAD is a 30-60-90 triangle.

we can use Pythagoras theorem to compute BC.

AngBis4.gsp

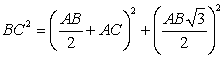
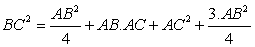
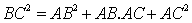(*2)

We said that BC is AB.k+AC.k (from *1), then

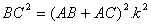
So 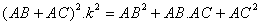  (*1 and *2)

Then 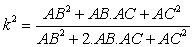     (*3)

When we use Theorem 2 for the length of the AA', we get

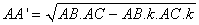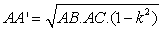   so   (*4)

Using *3 in the *4 gives us,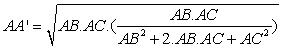 

then 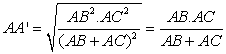   (*5)

Does *5 have a meaning?

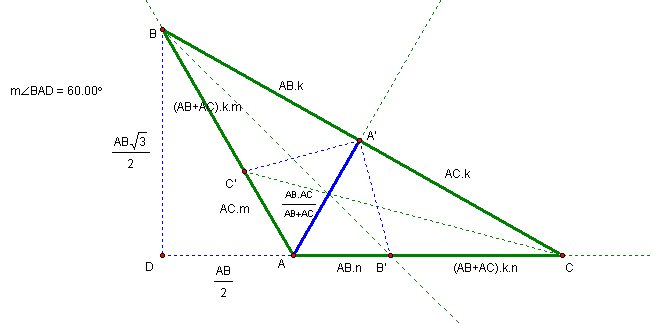
We need to look very carefully to see the meaning of the *5.

The ratio between AA' and A'C is

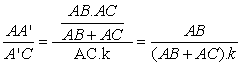         (*6)

And Ratio between AB' and B'C is

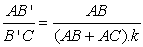      (*7)

Using *6 , *7  and Theorem 1, we conclude that A'B' is the Angle Bisector of Angle AA'C  (*8).

Similarly

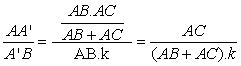  (*9)   and 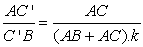     (*10)

Using *9 , *10  and Theorem 1, we conclude that A'C' is the Angle Bisector of Angle AA'B  (*11).

Using (*8) and (*11), we conclude that  Angle B'A'C' is 90 degrees.

 Turn Back to Emat 6690 Main Page