Finding Triangle from Given Medians

by Oktay Mercimek

I want to discuss third question for write-up, and question is

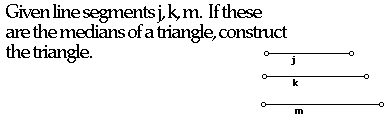
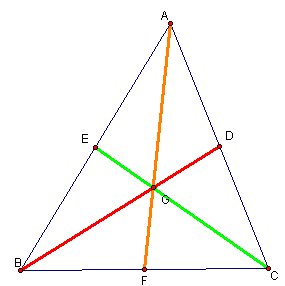
Since I didn't know how to solve this question, I started with a gsp drawing. I tried to find a relationship between triangle and medians and I tried several ideas about this relationship. First I drew a triangle and looked the the relationship between sides and medians

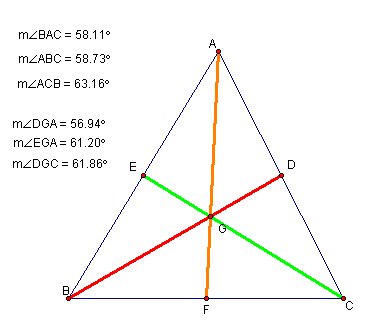
I couldn't see any relation between sides and medians. I tried several other things. They were also not successful ways to find a solution. And I decided to make a new triangle that consist of medians of the first triangle. and I explored the second triangle.

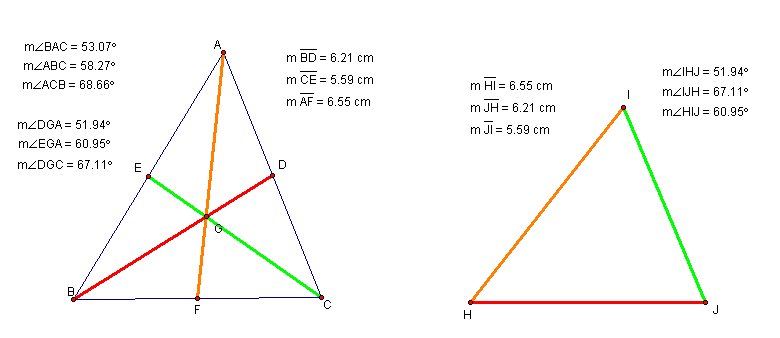
If you look at the picture carefully, you can see 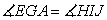. Sides of angle EGA is orange and green segments (original triangle), and sides of angle HIJ is orange and green segments (second triangle). We also see other relationships like

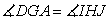  (red and orange segments)

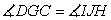  (red and green segments)

So angles between medians are same as angles between sides of second triangle.

Given lengths are medians. So to solve this problem, we need to find a transition from second triangle to first triangle.

We also know the relations between medians at the first triangle and these properties are

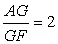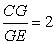  ,       and  .

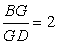Assume we have three given segments which are the medians of a triangle and we constructed the triangle which consist of these medians.

So we need to find the points, which trisect sides, on the segments of second triangle.

I used the Trisect tool that I made in Assignment 5. In fact trisecting each sides gives us more flexibility

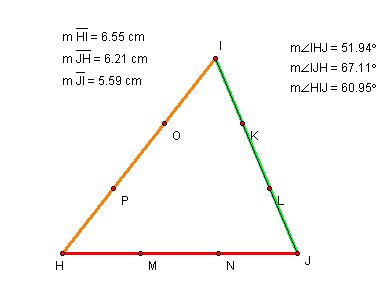
I created line IJ and line IH and draw a line at point I that is parallel to line HJ.

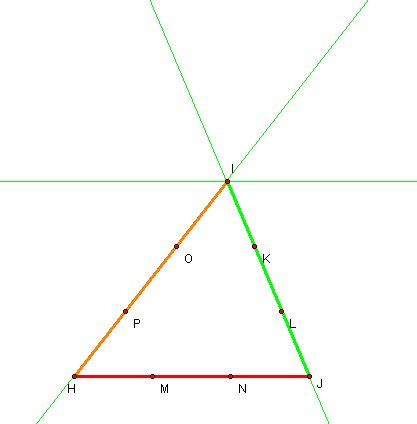
Since I didn't change the angles, situation is same as before, and Point I is ready for playing same role as point G at the first triangle.

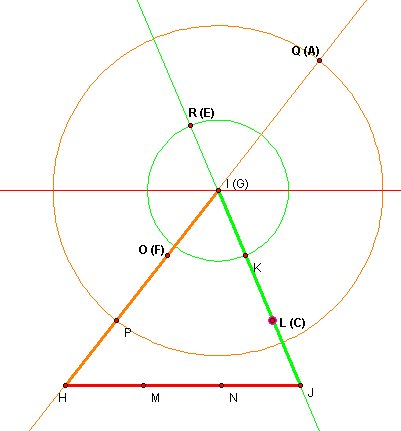
Let's start with point A. Point A is on the orange segment at first triangle so it also must be on orange segment. I draw a circle tah centered at point I and radius IP.

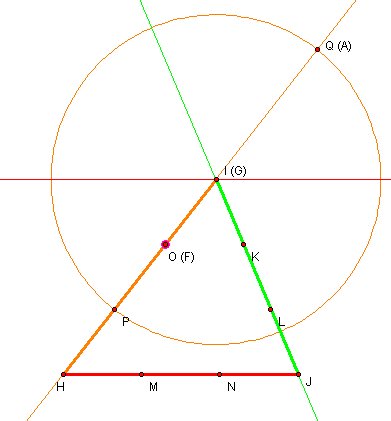
|IP| = |IQ| and in this case Point Q is in same place as Point A. Therefore point O is same place as point F.

We have to use obtuse angle between orange and green line to find the place of point C.

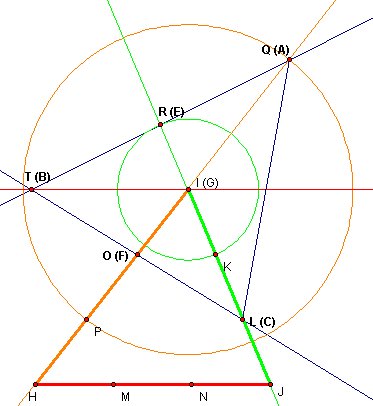
So Point L is same place as Point C , and we need Point E.

We have just find segment AC of original triangle. We know Point B is on line AE and line CF. so

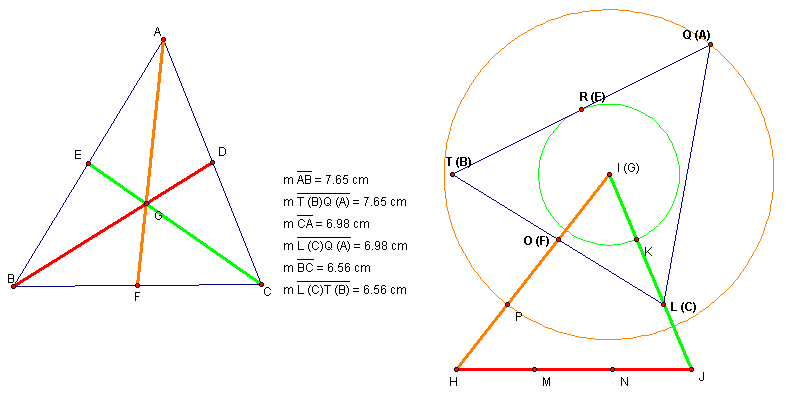
Now we found original triangle completely.

Let's check it out

You can download GSP file from HERE