Maximization with Spreadsheet

by Oktay Mercimek

In this write-up, I will explore maximization volume such as the lidless box formed from a 5x8 sheet with a square removed from each corner.

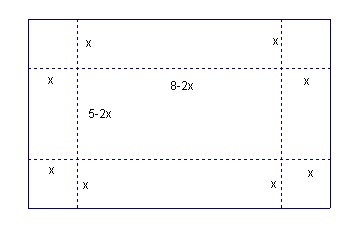
As we see here 2x cannot be larger then 5. We need to vary x values between 0 and 2.5 . We may increase x values step by step, so we need to decide how many steps we are necessary. For example, if we decide to make 1000 steps then the difference between every step will be

    .

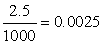If this amount is enough for us we can use 1000 steps for our spreadsheet file. If 0.0025 is large for us, then we can increase step value. Similarly if 0.0025 is small, then we can decrease step value.

Let's say we decided to make 1000 steps. So in this case we need values from 1 to 1000. To make this, simply write  1 in A1 box and write   =A1+1   in A2 box, copy A2 box first, Then choose boxes from A3 to A1000 and then use paste command.

After we created numbers from 1 to 1000, we need x, 5-2x and 8-2x values. For x values start with 0.0025 value and every other x value must be multiplication of step value and 0.0025. Write  A1*0.0025 in B1 and copy this value then choose boxes from B2 to B1000 and paste this A1*0.0025 value in them.

In same way C column must be in form of 5-2x so it is 5-2*B1 then copy this values to boxes from C2 to C1000 ,and D column must be in form of 8-2x so it is 8-2*B1 then then copy this values to boxes from D2 to D1000.

After we find x, 5-2x and 8-2x values, We need to multiply these there values so can find volume of box. Write  =B1*C1*D1 in E1 and copy it until E1000.

In E column, we see values are first increasing then decreasing. So it must be maximum somewhere. Until step 400, values increase and maximum value is 18, then values decrease. so the value we look for problem is 18, the maximum volume of the box.

You can find Excel fire HERE