Exploring Circumcenter

by Oktay Mercimek

I assume I ask these question to my audience and audience is a high school class

Q1: What is the circumcenter and circumcircle ?

A2: Circumcenter is the center of circumcircle that a triangle's vertexes lie on it.

Q2: How can we find circumcenter for given a triangle ABC ?    

A2: At first we should think about the definition of a circle.

    As we know circle is set of points that are equal distance (r) to a fixed point.

    So we are looking a circle that incident  with points A, B and C.

    Then center of circle must be equal distance from point A, B and C.

    Lets find points that equal distance from A and B.

Q3: How can we find points that equal distance to A and B.

A3: Midpoint of AB comes to mind and first. Let's think an isosceles triangle ABP that

    AB is the base of triangle.

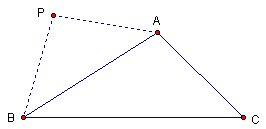
    If ABP is a isosceles triangle then a perpendicular line l  to Segment AB trough P is the bisector for segment AB.

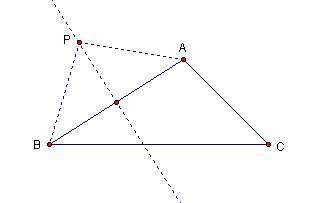
    Moreover every point on l  is equal distance to A and B.

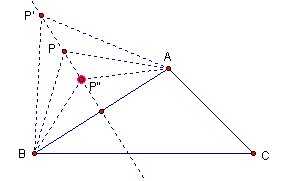
    We can apply same thought to AC. Let's m to be perpendicular bisector to AC.

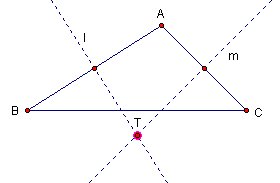
    So point T is equal distance from A, B and C.  

         |AT| =  |BT|  . Because T lies on l.

         and   |AT| = |TC| because T also lies on m.

        Then   |AT| = |BT| = |TC|

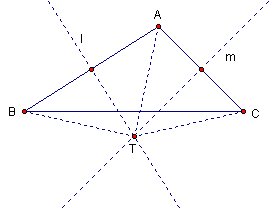
    Since  |BT| = |TC| , triangle BTC s a isosceles triangle and segment BC is the base of triangle.

   If we draw a perpendicular line n  to BC that incident with P, then this line has to be a perpendicular bisector to segment BC, and that is how the three perpendicular bisector of the sides of a triangle have to be concurrent.

    Let's turn to our question 2 . Since point T is equal distance from A, B and C ,we can define a circle that T is the center.

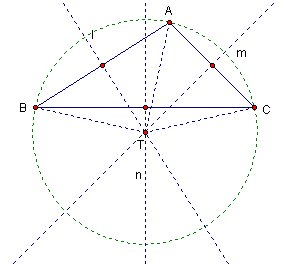
 And this is the circumcenter for triangle ABC. Click HERE for GSP demonstration.