A. Bouncing Barney
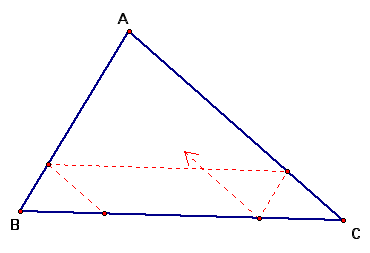
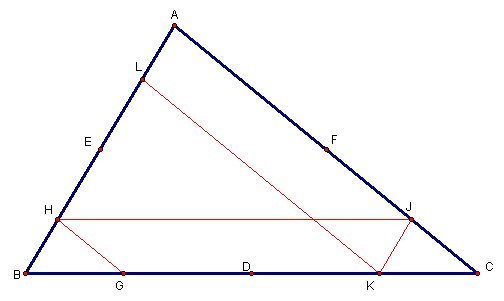
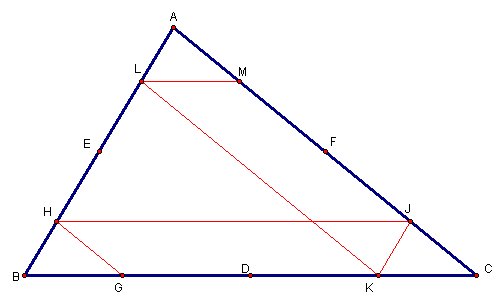
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall before returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.

Assume point D is the midpoint of segment BC, point E is midpoint of segment BA and point F is the midpoint of segment AC.
Assume Barney starts to walk from point G (that is on segment BC and different from point D) parallel to AC.
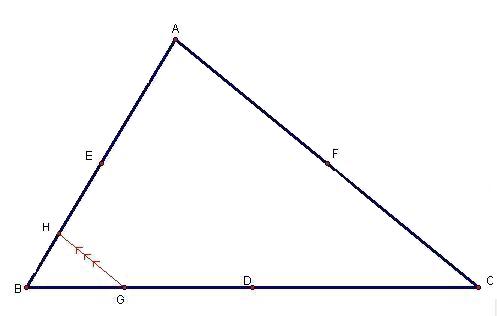
Since GH is parallel to AC, then
 is similar to
is similar to
 . , because
. , because
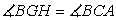 ,
, 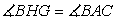 and
and
![]() is common in both
triange. Then
is common in both
triange. Then 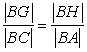 (1*)
(we will use this reasoning later in this document very frequently)
(1*)
(we will use this reasoning later in this document very frequently)
When he reaches AB at point H, he turns and walks parallel to BC
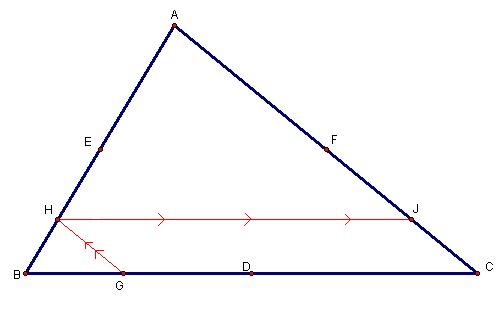
In this case, 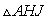 is similar to
is similar to
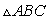 and
and
 (2*) .
(2*) .
Then he walks parallel to AB and reaches point K
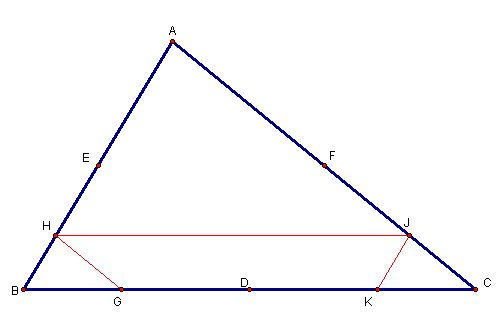
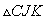 is similar to
is similar to
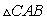 and
and
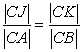 (3*).
(3*).
Then he moves toward AB and reaches to point L.
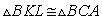 and
and
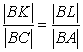 (4*)
(4*)
When he reaches AB at point L, he turns and walks parallel to BC
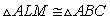 and
and
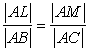 (5*)
(5*)
After he reaches point M, He will walk parallel to AB.
Will he reach to point G?
Claim: MG is parallel to AB
If we can prove 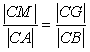 (6*)
then it means
(6*)
then it means 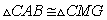 and then it means MG is
parallel to AB. {By the way I will prove
and then it means MG is
parallel to AB. {By the way I will prove
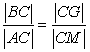 (6**) instead of
(6*) }
(6**) instead of
(6*) }
Let's organize what we found until now
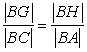 (1*) (1*) |
then 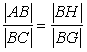 (1**). (1**). |
 (2*) (2*) |
then 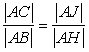 (2**) (2**) |
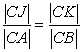 (3*) (3*) |
then 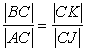 (3**)
(3**) |
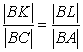 (4*) (4*) |
then 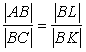 (4**)
(4**) |
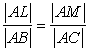 (5*) (5*) |
then 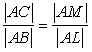 (5**)
(5**) |
We need to find to find a relationship between
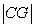 and
and 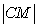 , in
order to prove equation (6**).
, in
order to prove equation (6**).
We don't see these terms in table, but we see complementary sides of
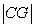 and
and 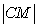 which are
which are 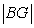 and
and
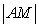 respectively.
respectively.
Trick 1:
So let's write 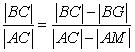 instead of (6**)
instead of (6**)Then It gives us
then
|
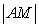 is in the (5**) and
is in the (5**) and
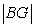 is in the (1**) so we need use them.
is in the (1**) so we need use them.
We don't have 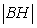 and
and
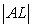 . We need to apply trick 1 again.
. We need to apply trick 1 again.
When we apply trick 1 to (2**),
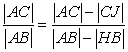 and
and
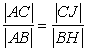 (2***)
(2***)
When we apply trick 1 to (4**),
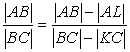 and
and
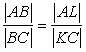 (4***)
(4***)
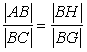 (1**) (1**) |
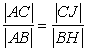 (2***) (2***) |
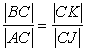 (3**)
(3**) |
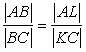 (4***) (4***) |
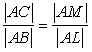 (5**)
(5**) |
It seems like we have all terms we need to use.
If we multiply left sides with each other and right sides with each other, then equation doesn't change and we have
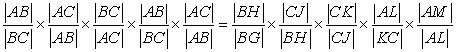
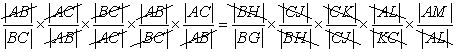
So we get 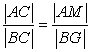 . We just
proved equation (6***).
. We just
proved equation (6***).
Then our claim is correct and MG is parallel AB.
It means Barney is returning to point where he started.
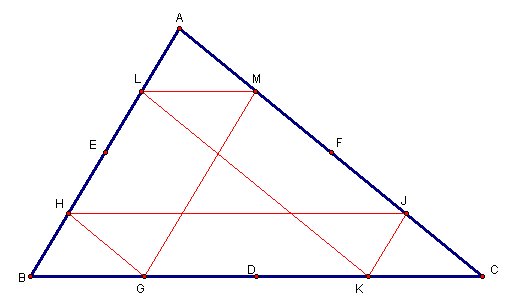
Let's try to find the length of this path.
We know LM is parallel to BG and BL is parallel to MG, then BGML is a parallelogram where |BG|=|LM| and |BL|=|GM| (A*)
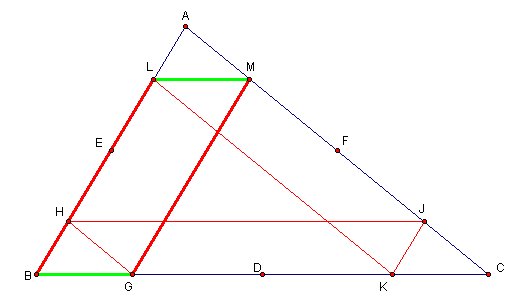
AL is parallel to JK and AJ is parallel to LK, then AJKL is a parallelogram where |AJ|=|LK| and |AL|=|JK| (B*)
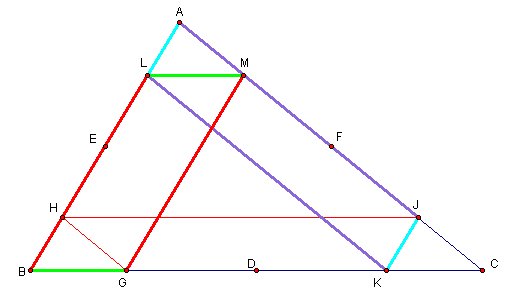
HJ is parallel to GC and HG is parallel to JC, then HGCJ is a parallelogram where |HJ|=|GC| and |HG|=|JC| (C*)
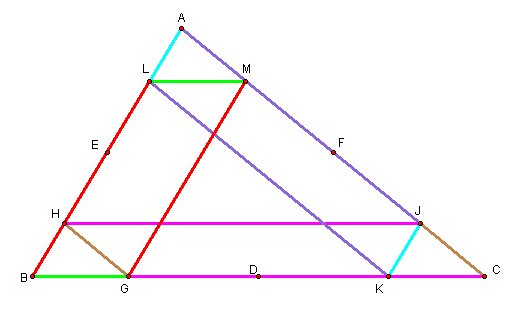
Could you see that path of Barney is same as perimeter of triangle?
PATH= |GM|+|ML|+|LK|+|KJ|+|JH|+|HG| = |BL|+|BG|+|AJ|+|AL|+|GC|+|JC| (from A* , B* and C*)
|AB=|BL|+|AL| , |BC|=|BG|+|GC| and |AC|=|AJ|+|JC|
then PATH= |AB|+|BC|+|AC|
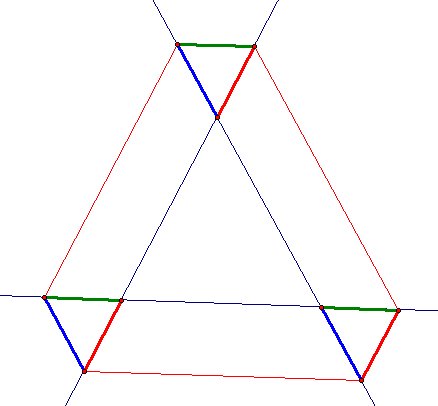
Starting From Outside Of Triangle?
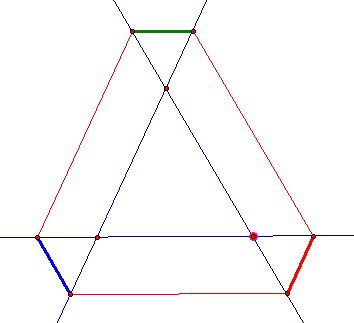
This GSP sketch shows that Barney will turn the starting point even when he starts outside of triangle.
However sum of path is clearly much more from perimeter of triangle. There may be a relationship though.
I colored some segments first
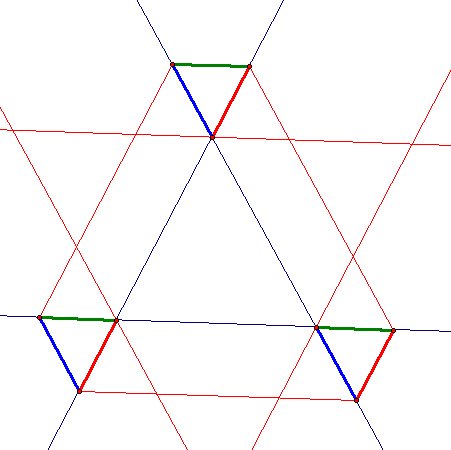
It seems like there is a relationship. I wanted to what happen when I draw some extra parallel lines.
as a result
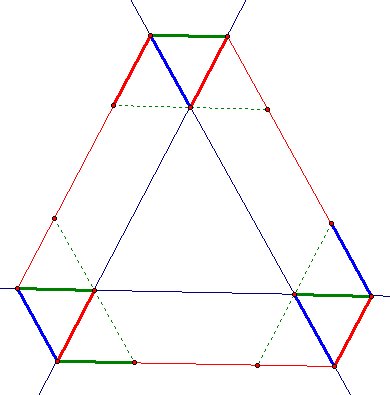
Did you see he relationship?
let's label the segment, and put same letter on equal sides
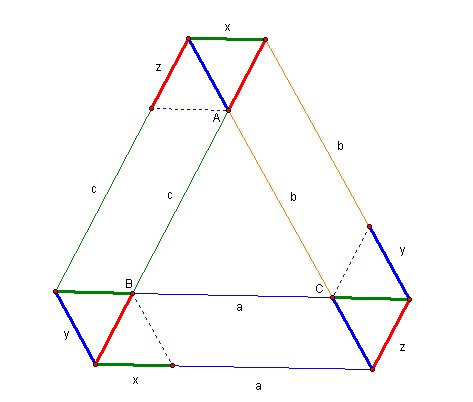
As you see in the picture, part of Barney is a+b+c+2x+2y+2z and perimeter of circle is a+b+c.
So path is 2 perimeter of colored triangles longer than perimeter of triangle ABC.
It can be also said that
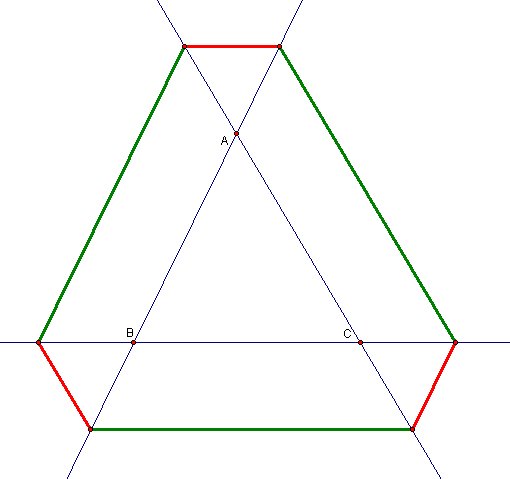
subtraction of sum of red segments from sum of green segments gives us perimeter of circle.