Oktay Mercimek, EMAT 6690

 

Estimating Volume of an Irregular Solid

This write up is a additional exploration for Volume of An Irregular Solid project and I recommend you to read that project first. there are a lot of way to find the volume of regular shapes but there is no certain way to compute the volume of irregular shapes. In this write up I want to use little different way find the volume of waste. The difference will be the computation. Computation will be made by Geometer's Sketchpad in a completely automated way and the main idea is keeping the process as simple as possible.

 

SECOND APPROACH FOR AVERAGE VALUE

(Probably this approach is much more appropriate for high school students. That's why I put my first approach to end of this page)

Now I want to make another argument about what can be average amount of volume. I will use only Geometer's Sketch Pad 's most basic functions.

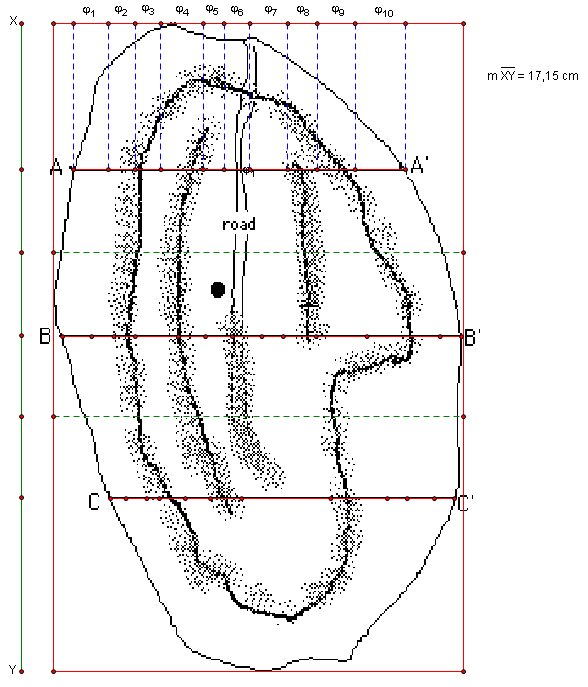
1.First I will define an polygon interior for three cross- section and I will find area using GSP

a. copy pictures and paste them into a gsp file.




b. then draw lines around cross-section (use only one direction, e.g. clockwise)



(half progress)

Tip: In GSP you don”t need to draw lines to define an polygon interior. We draw lines to see how well points cover the picture.



  1. After choosing lines , select only points ( one direction again to select points and this warning is much more important in this step)




d. select “Polygon Interior” under “Construct” menu and then “Area” under “Measure” menu.



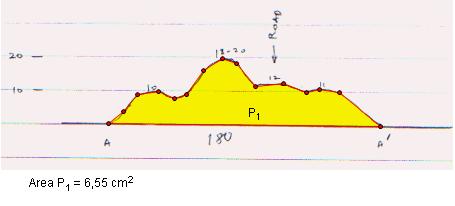
    Area result may vary related with what kind of GSP settings you use









e. repeat same steps from a to e for BB' and CC'




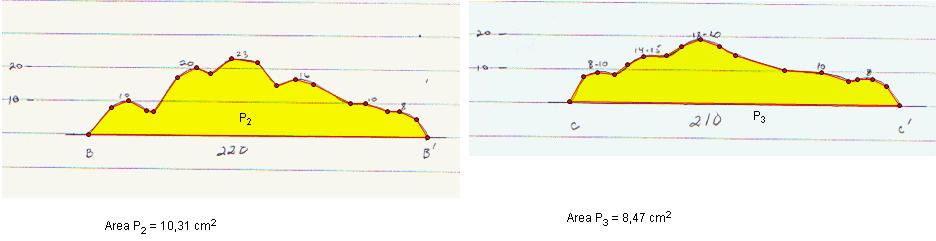
2. Let's find area factor for each one

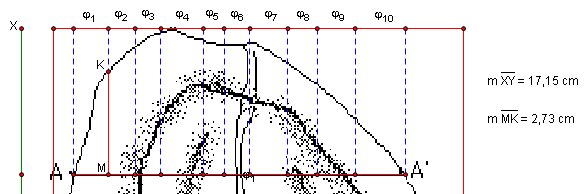
a. Draw AA' line


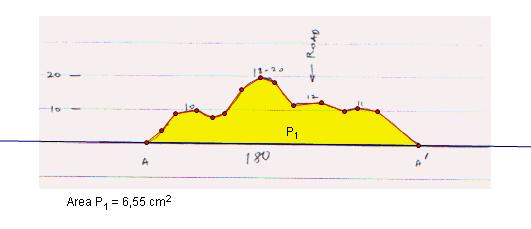
b. Draw lines perpendicular to AA' at points A and A' ( select line AA' , point A and point A' then select “perpendicular lines” under “construct” menu) and define point K that is intersection of one of the perpendicular lines and 20' feet line.


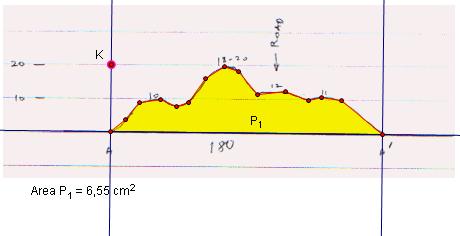
then draw a line from point K that is parallel to line AA' and define point M


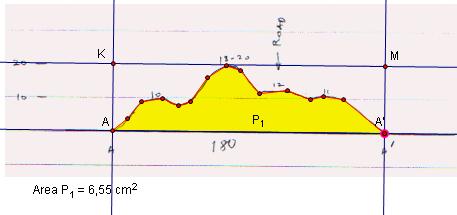
now we can construct rectangular interior for rectangle AA'KM and find area.


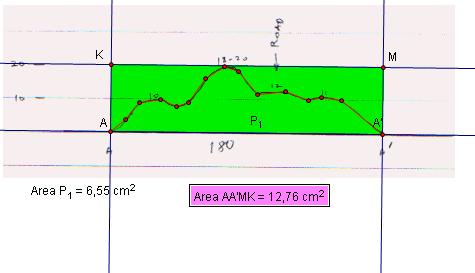
We know real area of rectangle AA'MK is 20*180=3600 square foot so the ratio between real area and drawing's are is 3600/12,76=282,09 will remain fixed for every sample area in this picture. GSP found area of P1 as 6,55 cm2.  To find (area of P1),

 and  (RealAreaP1)=282,09*6,55=1848,58

apply same system for BB' and CC'





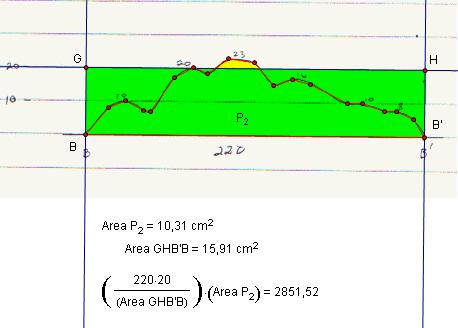
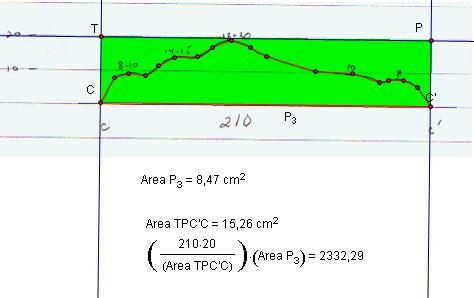
If we assume each cross-section is in the center of one third of the pile


then length for each section is 150 ft.

 so Volume of Section 1 is 150*1848,58=277287 cubic feet,

Volume of Section 2 is 150*2851,52=427728

and Volume of Section 3 is 150*2332,29=349843,5. total volume is 39068,83 cubic yards. A GSP file that includes all process

 

My first and worse approach (engineers may like it though! )

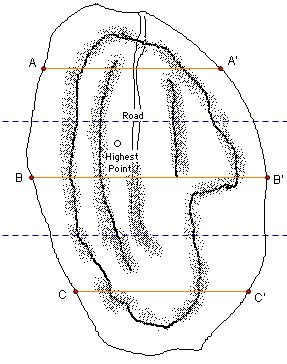
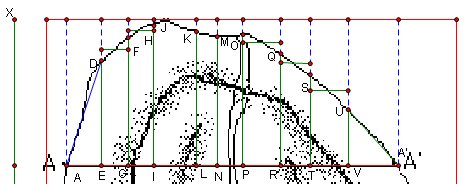
I first thought to share the whole region into 5 parts.







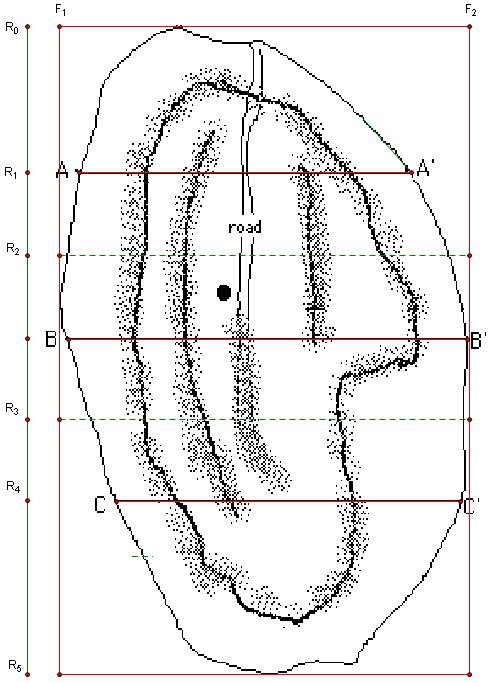
← Image1













These parts are:

  1. Part between R0 and R1

  2. Part between R1 and R2

  3. Part between R2 and R3

  4. Part between R3 and R4

  5. Part between R4 and R5










First I defined appropriate points on three cross-section.

















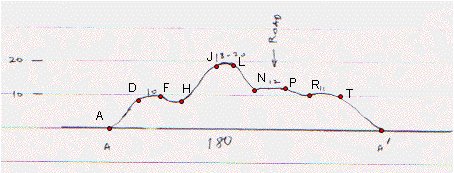
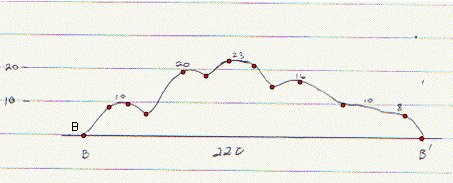
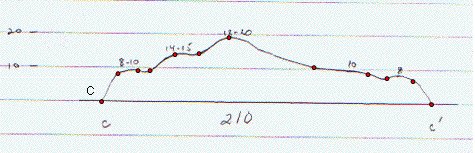
To see whether this selection true or not, I drew segments.










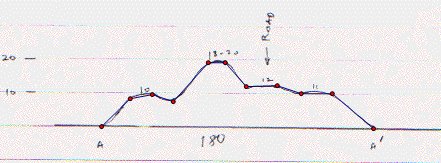
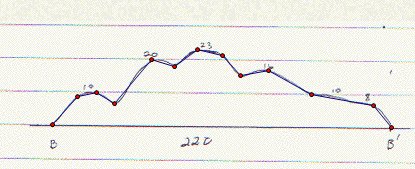
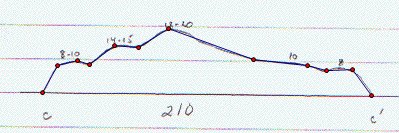
Next drawings demonstrate my ideas to find volume.

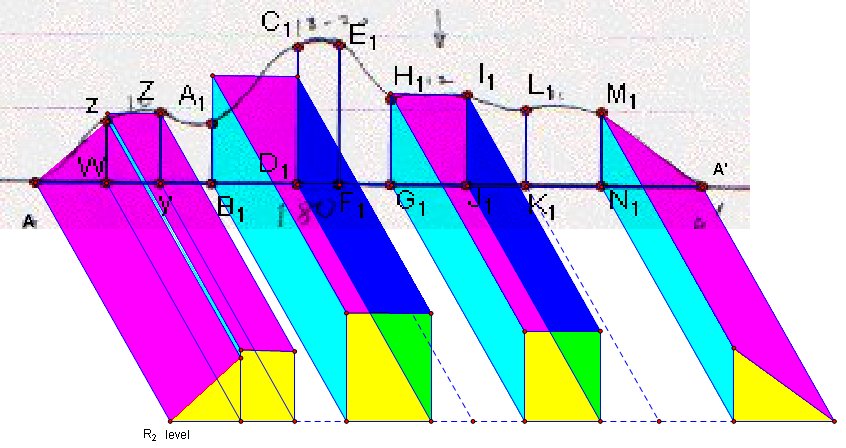
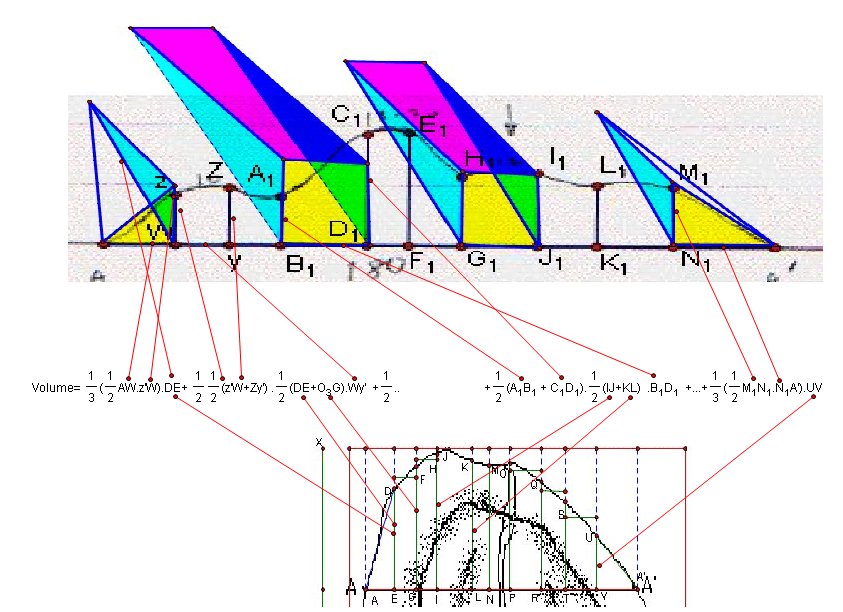
drawing1: this is my system to approximate first (and last) part. I thought sides as pyramids and middle as prisms. In the middle area, I took average height to find heights of prisms so it made my job easier!

You can see average issue below on points between B1 and C1 . Actually I didn't draw all lines on all drawings to show you a more clear picture.


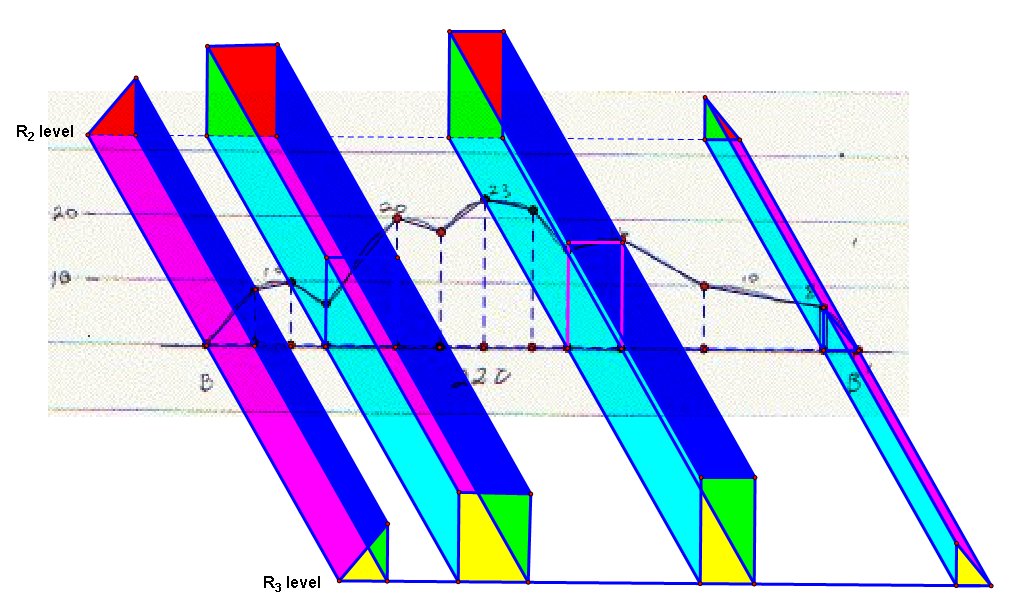
drawing2: This is my system to find volume Part 2 between R1 and R2 . I used AA' cross-section to find heights of this section. Part 4 is also similar, only difference is I used naturally CC' cross-section.


drawing 3: and this is for part 3, Part between R2 and R3. BB' cross-section is in the middle and I used heights on BB' cross-section.




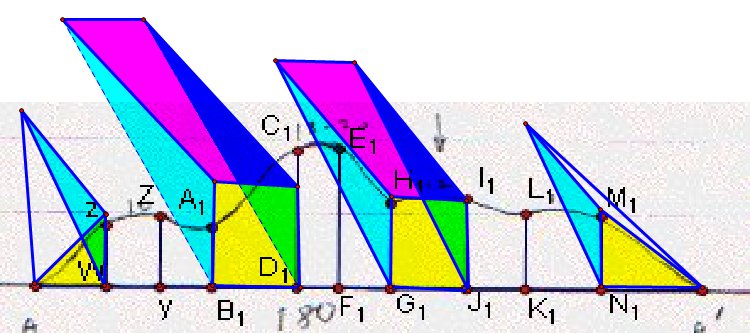
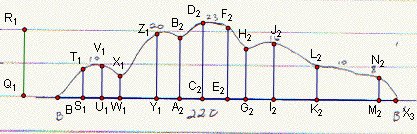
Then I started with part 1, between R0 and R1 . The problem was how to transfer these points to big picture, and I decided to use similarity of triangles.

The picture below shows how I used similarity.

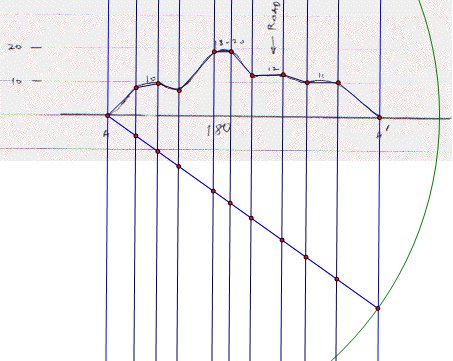  1. I drew a circle centered A with radius AA'( red segment, the one in the image 1)

  2. I drew perpendicular lines to AA'.

  3. then assigned the intersection points.

In this picture I used parallel lines to compare AA' on the cross-section picture an AA' on the image 1(big picture).















  1. Then I transferred this lengths to image 1 using circles. (I did same things also for BB' and CC' )




5. I used XY segment to find vertical length on image1. We know XY actually refers to 450 ft.

6. I treated as a pyramid to section φ1 and φ10 , and as a prism to section φ2 through φ9 .







































For example,

and since we know XY and KM we can find easily what is the real value of KM.

GSP can also do this computation.





I used almost exactly same system to find heights along AA' :


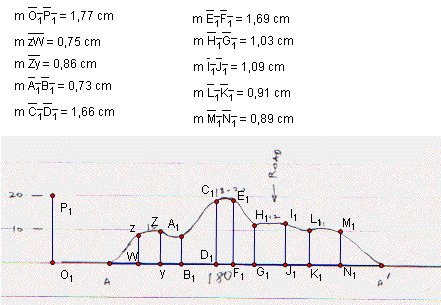
we can set same equation here


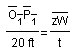
and we can apply same equation just simply changing O1P1 by zW, ZY, ..., and M1N1.


and we also need more measurement


we would be ready to go further when we measure vertical length like DE,FG, ... ,UV







We did all necessary measurement to find volume of first part so we can compute volume.


so V1=2644,81 cubic yards


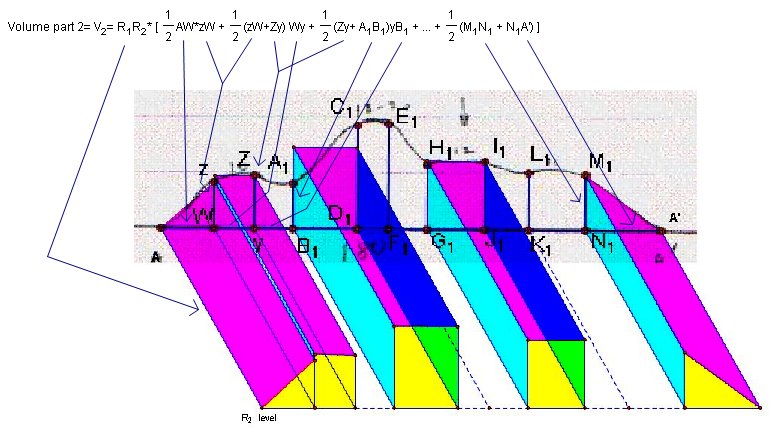
V2=3941,06 cubic yards



Part3:







V3= 11819,85 cubic yards.



Part 4 is similar to Part 2, and


V4 = 5037,32 cubic yards.



Part 5 is similar to Part1, and





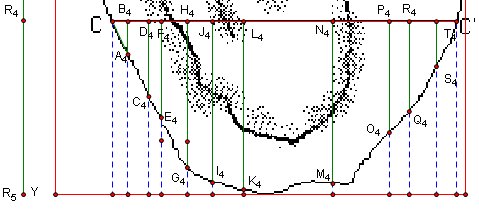
V5 =2785,16

Then total volume approximation is 26228. I tried to be as near as possible to real volume amount.