Oktay Mercimek, EMAT 6690
Step 6: Cassegrain Telescope with Pictures
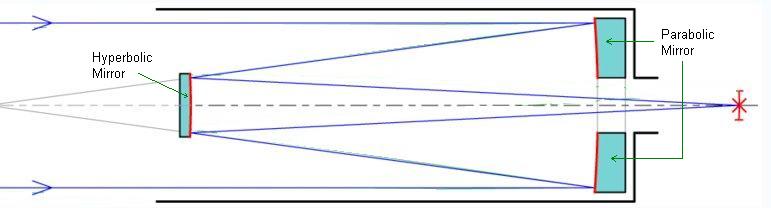
Cassegrain telescope has both parabolic and hyperbolic mirror. Parabolic mirror works same as in the Newton Telescope. Parabolic, primary, mirror collects light rays at its focus and hyperbolic mirror that reflects light back down through a hole in the primary.
Lets start with regular parabolic mirror construction. we also need a curve to demonstrate the hyperbolic mirror. because of this, we may need to construct two separate rays.
Lets start with constructing parabolic mirror as in the Newtonian telescope.
To do that, we need two parallel lines to be the sides of the telescope, two rays to demonstrate light rays, a focus and a directrix for parabolic mirror.
Here P is the focus point of the parabola (you cant drag it but you can drag point J to change the position of the point P).
Ray EG and ray FG will be the rays to construct parabola and the they will also demonstrate the light rays. You can also drag point E and point F.
Now we are ready to construct our parabolic mirror.
As you remember from the parabolic mirror construction, we need to create segment PF and segment PE. then construct perpendicular bisector of these segments.
As we learned in the parabola page, Points M and N are on the Parabola (when we constructed locus of point M and N) Ray HN will reflect through NP and ray GM will reflect through MP
Now we can construct Hyperbolic Mirror. To do that, we need two focus points and a circle. But as we discussed in the hyperbola reflection properties, we have to use Point P as one of our focus points because Light rays come to this point from several angles and we need to send them to the othe focus point.
Since we don't exactly know the radius of the circle, I made it changeable.
You can drag point Q to change the radius of the circle. Furthermore you can
drag point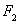 
. Orange and red rays intersect the
circle at two points, but we need to use points that are on the left half of the
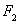circle because is on the
right side of the Point P (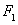
).
In this picture, point R is on the hyperbola, having
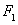and
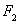as foci, because point R is
intersection of the perpendicular bisector of segment
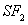and line SP. ( I temporarily deleted Ray HN
and some other things for a clear view)
And Locus of Point R and Point T is hyperbola
Little more clear picture:
In this sketch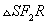 
is an isosceles triangle
and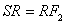 
. Therefore ray MR hits the
hyperbolic mirror and then reflects through
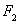
so the actual path of rays GM and HN are:
Now we can make fine settings which are Positions of Points P,
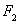and radius of circle (segment
IQ)
Segment CD was there from beginning of the project. I put it there because I thought there must be something that we can put the hyperbolic mirror on it (in real life!). so if you drag point Q to the little further than point I, you will see that hyperbolic mirrors became small enough to fit segment CD.
After we made the arrangements, we can create locus of paths of light rays.
In this file, you can drag point J to change position of Point P which is
focus of the parabola. Point P is also one of the focuses of the hyperbola. You
can also change the position of the
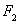which is the other focus of
the hyperbola. Segment IQ defines the radius of the circle which we used to
create hyperbola. therefore it also defines the size of the hyperbolic mirror.
You can drag point E and Point F to change the position of the light rays.
