Oktay Mercimek, EMAT 6690
Step 1: Parabola:
Let's start with the definition of parabola: Parabola is the set of all
points in the plane equidistant from a given line
(the conic section directrix)
and a given point
not on the line (the focus) (see
http://mathworld.wolfram.com/Parabola.html)
How can we use this definition to built a GSP model.
We need a line and a point
Then we need to find points that equidistant from from this line L and point P.
How can we do that?
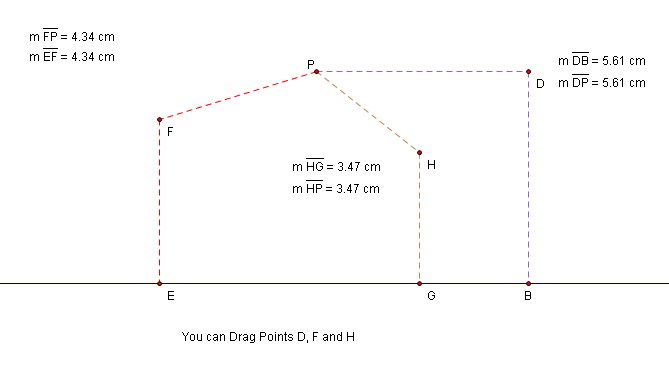
Let's construct several points and find the distance to point P and to the line
After we made these arrangements, It is clear that all these 3 points (D, F and H ) satisfy parabola definition.
Let's think what is common in the properties of Points D, F, and H
We know
,
, and
, then these triangles
are isosceles triangles. 
(Image
4)
Now problem is how to use this information to construct all points of parabola.
Let's turn to our starting point that we have only directrix and a point P (focus).
It is certain that we need a point the directrix in order to find points such as D, G, and H .
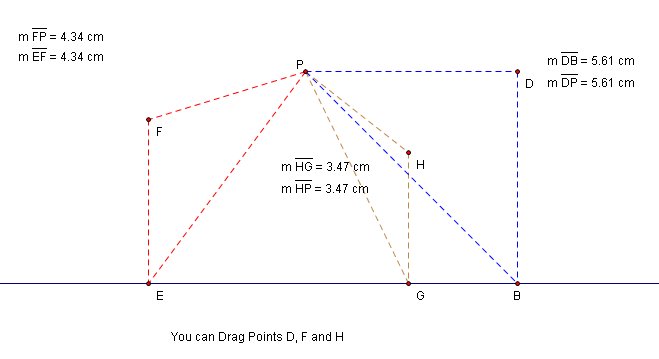
We also know points on the parabola such as D, G, and H are on the line that is perpendicular to directrix
As we know from Image 4, the segment connects point B and Point P is actually the base of the isosceles triangle.
And the Points D, G, and H are on the perpendicular bisector of this base segment
Since Points D, G, and H are on the
Then these points are actually on the intersection of these two lines.
You can drag Point B to see traces of Point C or you can click on the "Animate Point B" button. (You can refresh page to erase traces)
Constructions until this point will hopefully help us to understand reflection properties of parabolas.
In this part, we will explore the reflection of rays that are especially perpendicular to the directrix or equivalently rays that are parallel to the axis of symmetry.
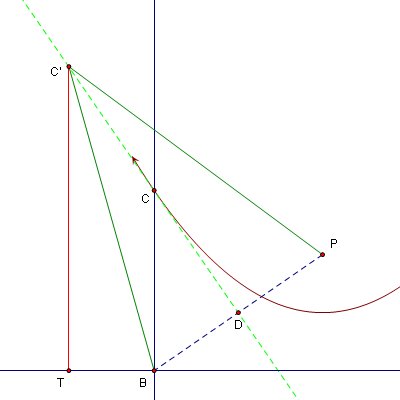Image 5
At this point, it is important to see that CD is tangent to parabola at Point C.
Assume another point of the parabola, point C', is on the line CD. According to our assumption C' is on the parabola so |C'T|=|C'P| (1*).
C' is on the bisector of segment BP so |C'P|=|C'B| (2*).
(1*) and (2*) requires |C'T|=|C'B|. As you can see in Image 5, it is not possible. Therefore it is a contradiction.
Then there is no second point on both on Line CD and on the parabola. Thus line CD is tangent to parabola.
Since we find the Line that is tangent to parabola at point C, we can apply basic reflection property: the angle of incidence equals the angle of reflection.
To be able to demonstrate this property, we will use a small trick with circle