Quadratic Equations

by Oktay Mercimek

In this write-up I will examine relationship between roots of Quadratic equation and c as in .

Let's say b=0, then .

If we graph this equation in the xc plane,

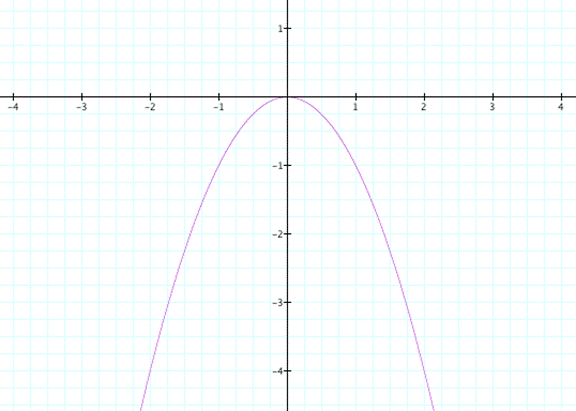
Adding parallel lines to x-axis will help to investigate for special c values.

To see what happens when c=1, We can add c=1 line to graph.

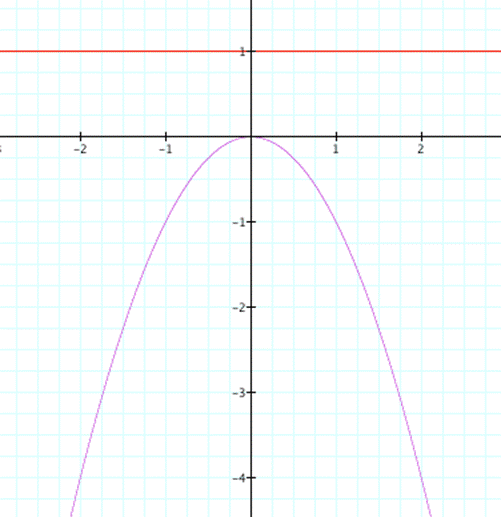red line is c=1

So for b=0 and c=1 , we don't have any root.

Let make c=-2 and see what happens.

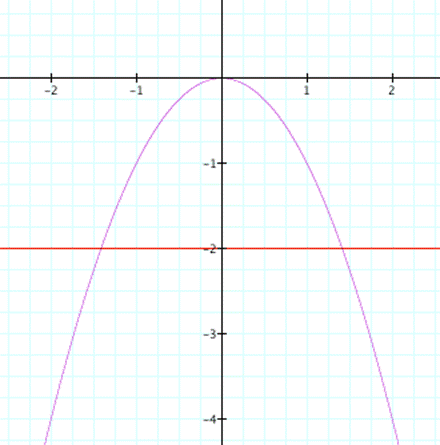red line is c=-2

The line intersects the curve at two points, one of them is between -2 and -1 , and other is between 1 and 2.

So for c=-2 we have two roots, one is negative and other is positive.

Let's say b=-4, then the equation becomes .

In this case graph of this equation in the xc plane

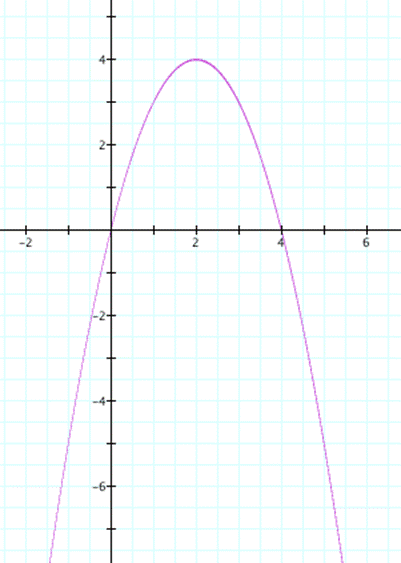
Let draw a few lines on this graph.

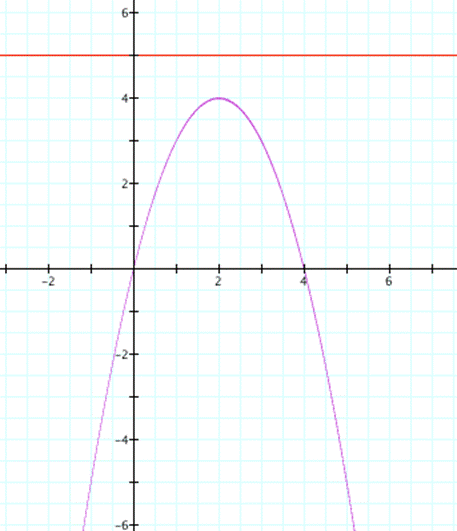red line is c=5

if b=-4 and c=5 then real equation is .

Since we don't see intersection between line and curve, this equation doesn't have a root.

Now let's try c=5

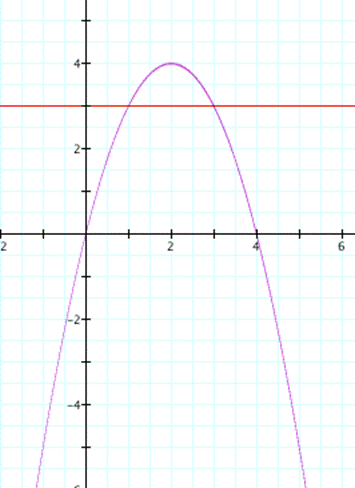red line is c=3

c=3 line intersects the curve in two positive points. So we have two positive roots. One of them is around 1 and other is around 3

For c=-1

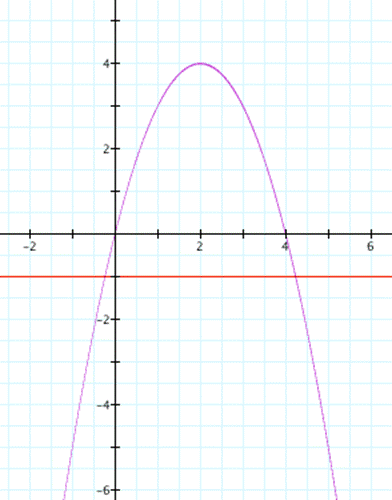red line is c=-1

so for c=-1, we have two roots. One is negative and other one is negative.

Let's arrange all information in a table to see relationship between c and roots.

b=0	c=1	No root
	c=-2	One negative and one positive root
b=-4	c=5	No root
	c=3	Two positive roots
	c=-1	One negative and one positive root

As you see in the table,

When we have a positive c then we have no root or two root of same sign.

When we have a negative c then we have a negative and a positive root.

It is also significant in graphs that curves always passing through point (0,0), so it means if c=0 then we always have x=0 as a root.