Altitudes of Triangle

by Oktay Mercimek

I wanted to investigate 12th problem from http://jwilson.coe.uga.edu/EMT668/Asmt8/EMT668.Assign8.html. This problem is very interesting to me because I have never seen an equation for parts of altitudes of a triangle.

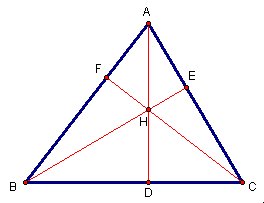
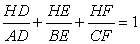          (*1)

        (*2)

I have tried almost everything I know. My first idea was using similarity because there are a lot of similar triangles in this problem.

For example,

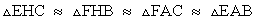and etc.

These similarities bring us

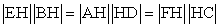
May be we can find more equation but I think all of them would be in form of multiplication like the one above.

So we need to try something other then similarity.

Second approach is using area for proofing our equation

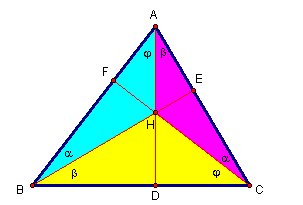
As we see in picture Area( ABC ) = Area( BHC ) + Area( AHC ) + Area( AHB )

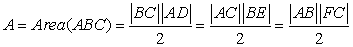             (*3)

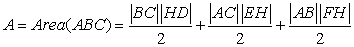             (*4)

Equation (*4) is better to go on it because equations (*1) and (*2) are in sum form.

Since 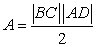  , we can write 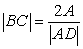in equation (*4). Similarly replace 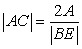 and 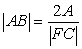in equation (*4).

So we have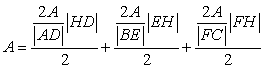

and this is equal to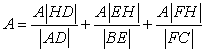

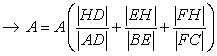  multiplying both side with 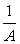gives us

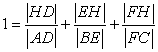   and this is equation (*1)

To proof equation (*2) will be easier with equation (*1)

we know 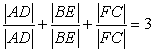So

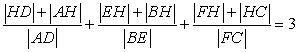
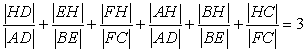  and using equation (*1)

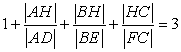
Finally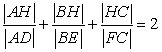

This assignment taught a lot of information to me. First of all, I learned a new equation for altitudes of triangle and then similarity is not the only way for proofing geometrical equations.