Pedal Triangles

by Oktay Mercimek

I would like to discuss the situation that Pedal point p is the Circumcenter of the triangle.

Let's draw a triangle, its circumcenter and circumcircle using the tool that we made at Assignment 5.

We can call this point P because we think it as Pedal Point. and draw pedal triangle.

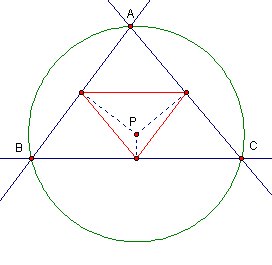
Question is "is this pedal triangle have another properties?"

We know circumcenter is equal distance from three vertexes.

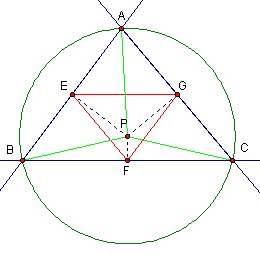
so |PA|=|PB|=|PC|

We know Triangle APB is a isosceles triangle and PE is perpendicular to AB.

Then it requires |AE|=|EB|.  (1)

We can apply same same logic to Triangle APC and Triangle BCP

then |AG|=|GC|  (2)   and  |BF|=|FC|   (3)

When we put together (1), (2) and (3), it means E, F and G are midpoints.

In this case Triangle EGF is medial triangle and pedal triangle. Click HERE to open GSP file of picture above

Let's look what happens when Triangle ABC is a obtuse triangle.

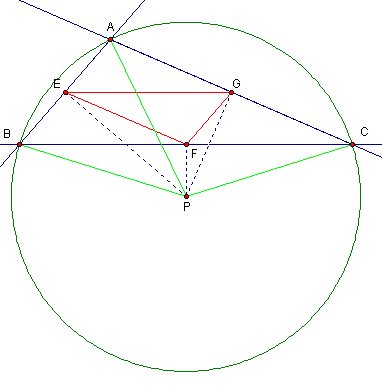
In this case P (or circumcenter) is outside of the main triangle.

However as you see in the picture there is not much change on properties of triangles.

Again Triangle APC is a isosceles triangle and PG is perpendicular to AC.

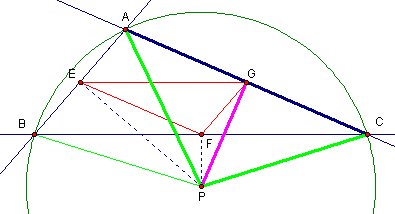
It makes Point G is a midpoint of segment AC.

Same discussion for Point F

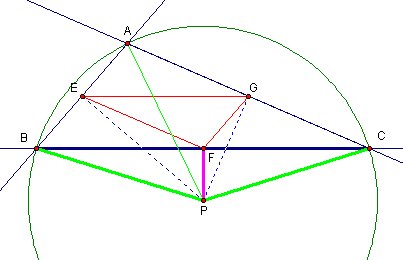
and for Point E

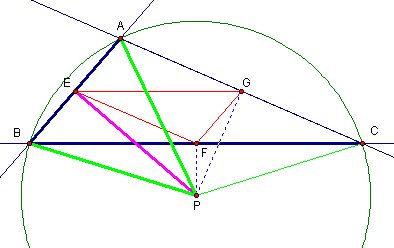
So these points are still midpoints.

then Triangle EFG is still a medial triangle.

So this investigations shows that if the pedal point is on the circumcenter, Pedal triangle is also a medial triangle.