1. Consider the triangle ABC. Choose a point inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Now we will explore (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles and various locations of P.

Now lets move the point P around and look at these values.

We will go back to our original triangle.

If you look carefully at the values you can see that the ratio of (AF)(BD)(CE)/(FB)(DC)(EA) = 1.

Conjecture: As long as your P remains inside the triangle the ratio of (AF)(BD)(CE)/(BF)(CD)(AE) = 1.

Proof: To prove this conjecture let's start with the triangle where point P is the centroid of the triangle and the values of (AF) (BD) (CE) and (BF) (CD) (AE):

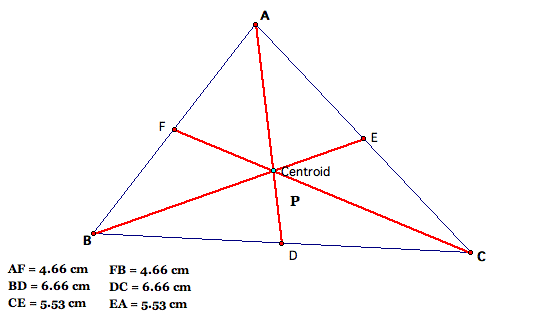
Look at the resemblance of the two sets of lengths.

Let's construct a parallel line of the line BC making sure that this line goes through the point A. Don't forget to extend the lines CF and BE so that we can easily see the similar triangles.

The purpose of this is so we can look at some of the similar triangles. These include:

AFG and BCF

AGP and CDP

AHE and BCE

BDP and AHP

Now we can look at the ratio of the similar triangles:

AH/BD = AP/DP

BF/FA = BC/AG

AG/CD = AP/DP

AE/EC = AH/CB

Since, as you can see AH/BD = AP/DP and AG/CD = AP/DP then we can say that AH/BD = AG/CD

Now if we multiply the ratios of these similar triangles, lets see what we get

(BD/CD)(AE/EC)(BF/FA) = (AG/AH)(AH/CB)(BC/AG)

This ratio is still 1.

So we have proven our conjecture.