

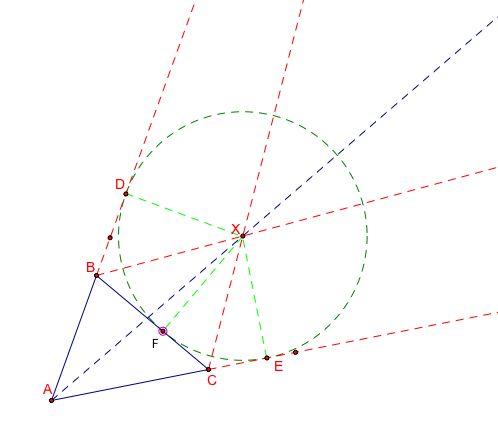
An x-circle is a circle whose center is a point of concurrency with one angle bisector of a triangle and the two angle bisectors of the opposite exterior angles. What makes this circle special is that it is also tangent to the lines on which the triangle is drawn. Therefore, every triangle has three x-circles.
Consider any triangle ABC. Extend AB and AC to form the exterior angles. Construct the angle bisectors for these angles and label the point of intersection of the bisectors X.
Construct the perpendicular line from X to line AB and label the point of intersection D. Construct the perpendicular line from X to line AC and label the point of intersection E. Finally, construct the perpendicular line from X to line segment BC and label the point of intersection F. By the definition of an angle bisector, we know that mDX = mFX and mEX = mFX. Hence, mDX = mEX.
Construct the ray AX. We now have two right triangles, ADX and AEX. Since mDX = mEX and the two triangles share the hypotenuse AX, we can conclude that the triangles are congruent. Thus, angle BAX is congruent to angle CAX.
In conclusion, point X must lie on the angle bisector of angle BAC and be the point of concurrency with one angle bisector of a triangle and the two angle bisectors of the opposite exterior angles.
For a visual aid of this proof, check out this GSP construction.
Now, to construct the x-circle, we must make sure that we can do so in such a way that the circle will be tangent to all three sides of the triangle. The trick here is to realize that it can be tangent to the lines on which the triangle sides lie. Using our construction from the previous section, we see that line segment DX can be used as our radius. Notice that since line segments EX and FX are the same length, each of these act as radii. Furthermore, since they were all constructed as perpendiculars, we know that the circle that passes through these points will be tangent to those lines. This GSP construction displays one of the x-circles. Try to find the other two!
The reciprocal of the radius of the incircle of a triangle is equal to the sum of the reciprocals of the radii of the x-circles for that triangle.
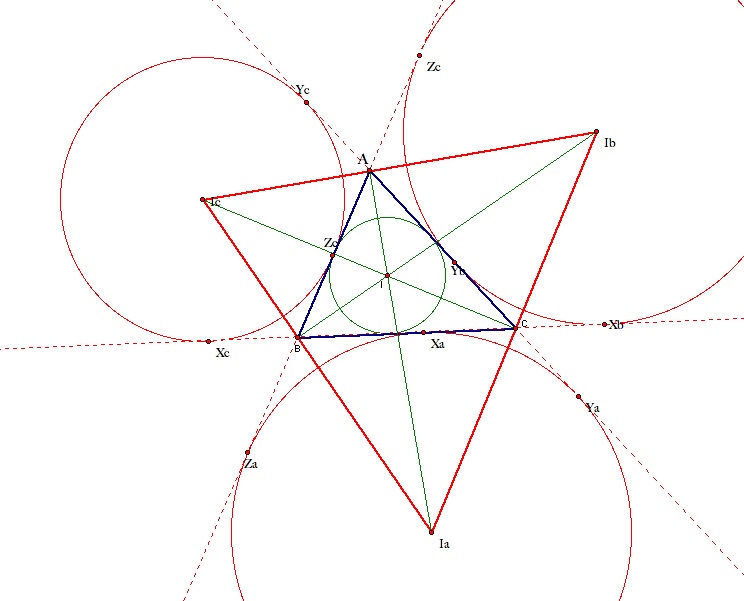
Let s be the semiperimeter of triangle ABC. Recall that the semiperimeter is equal to (a+b+c)/2 where a, b, and c are sides BC, AC, and AB respectively. Let r be the radius of the inscribed circle. Finally, let r_a be the radius of circle Ia, r_b the radius of circle Ib, and r_c the radius of circle Ic.
We know that the area of triangle ABC, denoted (ABC), is equal to sr. The reason for this is that we can separate triangle ABC into triangles IBC, ICA, and IAB. we know that these triangles all have altitudes equal to r and bases a, b, and c respectively. Hence, (IBC) = (ra)/2, (ICA) = (rb)/2, and (IAB) = (rc)/2. Therefore, (ABC) = (ra)/2 + (rb)/2 + (rc)/2 = r(a+b+c)/2 = rs.
Furthermore, (ABC) = (IaCA) + (IaBA) - (IaBC) = (r_a*b)/2 + (r_a*c)/2 - (r_a*a)/2 = (r_a)(b+c-a)/2 = (r_a)(s-a)/2. Similarly, (ABC) = (r_b)(s-b)/2 and (ABC) = (r_c)(s-c)/2. Using these equivalent statements for the area of triangle ABC, we can see that rs = (r_a)(s-a)/2 which implies that r/r_a = (s-a)/2s. Similarly, r/r_b = (s-b)/2s and r/r_c = (s-c)/2s.
We are trying to prove
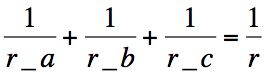
which is equivalent to the equation
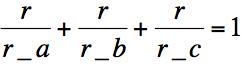
However, since we have the area equivalences above, we see that
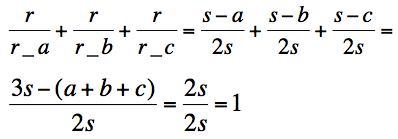
QED.