

A parabola is the set of points equidistant from a line and a fixed point. This line is called the directrix and the point is called the focus. There are several ways you can use this definition to construct parabolas from the Cartesian coordinate system, to paper folding, to Geometer's Sketchpad (GSP). the benefit of using GSP has to do with the fact that in GSP, points can be animated, loci can be traced, and the explorations can go much more quickly than if you had to draw or fold everything yourself.
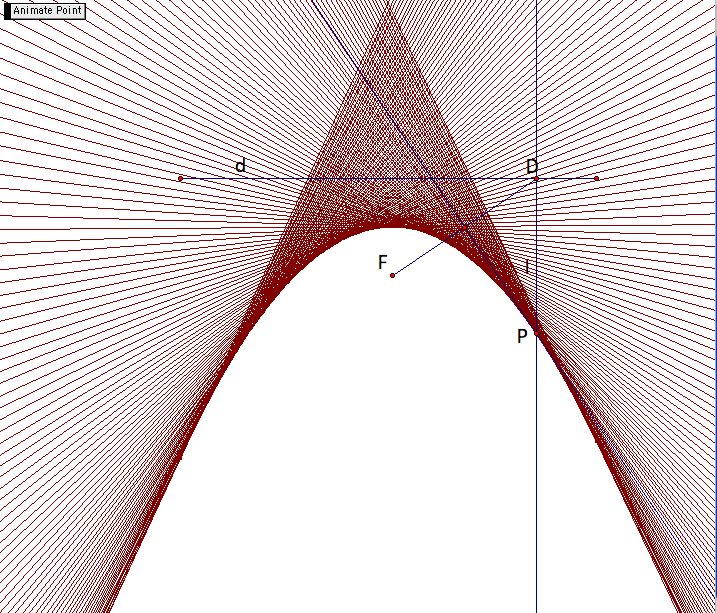
To construct the parabola, first construct a line segment and a point not on the line. This segment will serve as the directrix, d, and the point the focus, F. Choose a point on the directrix, D, and construct the perpendicular line to d through D and name this line l. Also construct the line segment FD. Construct the perpendicular bisector to FD. This bisector will intersect line l. Call this point of intersection P.
Notice, that as D is moved along d, the point P also moves. In fact, the locus of points of P will create a portion of a parabola. A way to see this is to animate the point D and trace P. In order to see the whole parabola, you can trace the perpendicular bisector of FD, or have GSP display its locus of point. You can try this construction yourself or see my GSP file.
In order to construct an ellipse or a hyperbola, instead of using a line as the directrix, you can use a circle. To construct the ellipse, first construct a circle, d, and a point inside the circle, but different from the center, and name this point F. Choose a point on the circle, a.k.a. the directrix, and name this point D. Draw the line through D and the center of the circle and construct the line segment FD. Construct the perpendicular bisector to FD. This segment will intersect the line through the center. Call the point of intersection P.
Notice, that as D is moved along circle d, the point P also moves. In fact, the locus of points of P will create an ellipse. A way to see this is to animate the point D and trace P. You can see this trace on my GSP document and play with the position of F to see what you can do to the ellipse as F moves closer and farther away from the center. However, to keep the trace an ellipse, F must stay inside of the circle.
If F moves outside of the circle, the locus of points will become a hyperbola. To further the investigation for the hyperbola, you can have GSP display the locus of point for the perpendicular bisector of FD to see the hyperbola more clearly.

My GSP
document for the hyperbola construction will allow you to
experiment with the position of F so see how the hyperbola will
change as F moves further away from the circle. It is also interesting
to see how the perpendicular bisector acts as D moves around the
circle.