

This investigation begins with the construction of an acute triangle along with its circumcircle. Also included is the orthocenter as well as the three altitudes of the triangle extended so that they intersect the circumcircle.
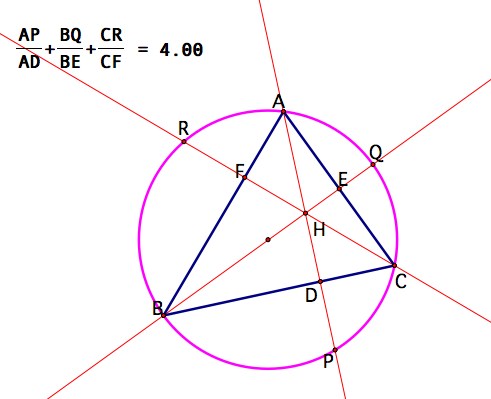
One thing that I found out was that the ratios above, when added together, would always be equal to 4. But why did that have to happen?
To prove this, I first started with the idea that segments AP, BQ, and CR could be divided into the sums AD + DP, BE + EQ, and CF + FR respectively. By doing this, the fractions could be reduced to 1 + (DP/AD), 1 + (EQ/BE), and 1 + (FR/CR), which in turn reduced my equation to 3 + (DP/AD) + (EQ/BE) + (FR/CR). Hence the problem reduced to showing that (DP/AD) + (EQ/BE) + (FR/CF) = 1.
Now the area of triangle ABC can be expressed in three different ways. Because AP, BQ, and CR are altitudes, the area can be expressed as A = .5(AD)(BC) = .5(CF)(AB) = .5(BE)(AC). Using these expressions, I was able to simplify (DP/AD) + (EQ/BE) + (FR/CF) to {(DP*BC) + (EQ*AC) + (FR*AB)} / 2A.
Here is where the proof gets exciting, because if I was able to show that (DP*BC) + (EQ*AC) + (FR*AB) was actually equivalent to 2A, I would be done! In order to do this, I turned to congruent triangles. I wanted to show that triangle BHD was congruent to triangle BPD. By doing this, I could conclude that segment DH was congruent to segment DP. Why did I want to do this? Well, if that was true, then the area of triangle BHC would be equal to .5(DP)(BC). Then I could use a similar argument to show that the areas of triangles BHA and CHA were equal to .5(FR)(AB) and .5(EQ)(AC) respectively and then I would have completed the proof!
So, getting back to triangles BHD and BPD, firstly, they share side BD. Furthermore, angles HDB and PDB are right angles. Finally, angle HBD is congruent to angle PBD. The reason for this final congruence has to do with inscribed angles.
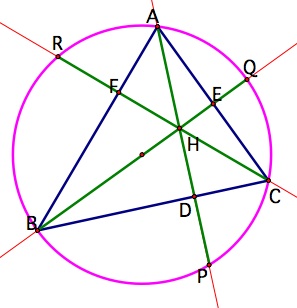
First notice that the angles AHE and CHD are vertical, and hence congruent. Then since angles HEA and HDB are 90 degrees, angles EAH and DBH must be congruent. That implies that arc QC must be congruent to arc PC. Therefore, the two inscribed angles QBC and PBC are congruent. Thus, by SAS, triangles BHD and BPD are congruent.
To summarize this discussion,
