

Barney is in a triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB.
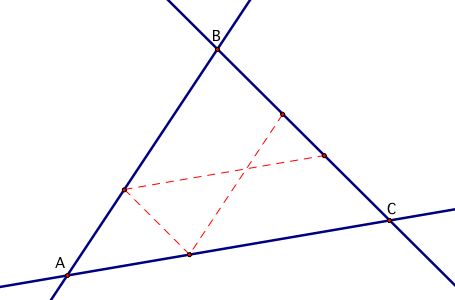
Conjecture 1: Barney will reach his starting point in 6 walks.
To investigate this, I first created a GSP file that modeled the sitiuation. It seemed like no matter where I put the initial point, the number of paths was always 6. Check out my sketch and see if you can come up with the same conjecture.
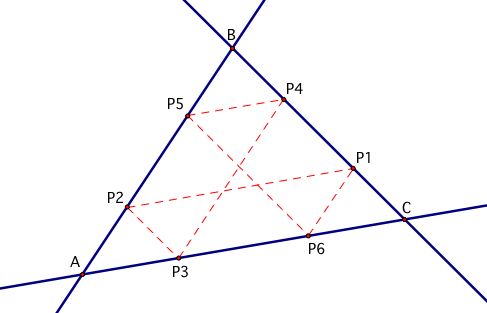
So the question becomes, how can this be proved?
Segements P1P2 and AC are parallel as are segments P2P3 and BC. Therefore, quadrilateral P1P2P3C is a parallelogram, which implies mP3C = m P2P1. A similar argument can show that quadrilateral P2P3BP4 is also a parallelogram and mP2B = mP3P4. Furthermore, the parallel properties of the segments imply that angles BP2P1 and P4P3C are congruent. By SAS, triangles BP2P1 and P4P3C are congruent.
Using this argument with segments P5P6 and P1P2, we can prove that triangles P5AP6 and P4P3C are also congruent. This implies that triangles BP2P1 and P5AP6 are congruent.
Now suppose when we draw the path from P6, parallel to AB to side BC, it intersects BC at point P7. We then continue Barney's path from P7, parallel to AC to side AB. Call this point of intersection P8. Using a similar argument as above, we can show that triangles P5AP6 and BP8P7 are congruent. Therefore, we can conclude that triangles BP2P1 and BP8P7 are congruent.
However, this means that segements P2P1 and P8P7 are congruent. But the only way for this to happen is for P7 = P1 since both P7 and P1 must lie on segment AC.
Conjecture 2: The path length is equal to the perimeter of the triangle when P1 is between points B and C.
The distance between P2 and P3 is equivalent to the distance between P1 and C. The distance between P5 and P6 is equivalent to the distance between P1 and B. Therefore, these two parts of the path are equal to BC.
Similarly, the distance between P1 and P6 is equivalent to the distance between P2 and A. The distance between P3 and P4 is equivalent to the distance between P2 and B. Therefore, these two parts of the path are equal to AB.
Finally, the distance between P4 and P5 is equivalent to the distance between P3 and A. The distance between P1 and P2 is equivalent to the distance between P3 and C. Therefore, these two parts of the path are equal to AC.
Now why are all of these lengths equivalent? I will show one example and leave the others to you (they are all the same, so don't worry!).
The line P1P2 is parallel to the line AC. Therefore, angle P6P1P2 is equivalent to P1P6C. Furthermore, since the lines P1P6 and AB are parallel, angles P1P6C and P2AP3 are equivalent. So, angles P6P1P2 and P2AP3 are equivalent. A similar argument can be used to show that angles P1P2A and P1P6A are equivalent. Hence, quadrilateral P1P2AP6 is a parallelogram which implies that segments P2A and P1P6 as well as segments P1P2 and P6A are equivalent.
Note: The length of the path will be different when P1 is outside the triangle, one a vertex, or on a midpoint of one of the sides.
When P1 is outside of the triangle, the length of the path is equal to the perimeter plus twice the summ of the lengths of the segments AP3, BP5, and CP1.
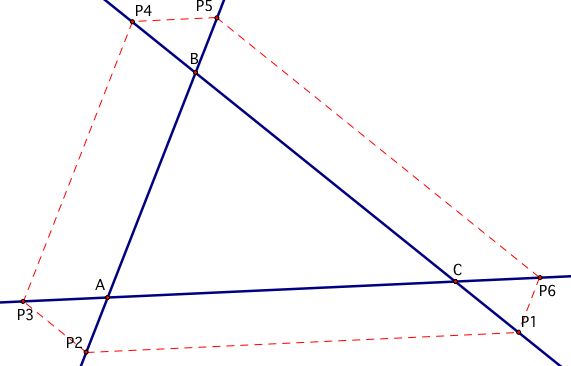
Notice that the paths create parallelograms surrounding the triangle where the segment P1P2 is equivalent to AC plus AP3. But, segment P4P5 is also equivalent to AP3! Looking at the diagram in this way should make the statement above clear.
When P1 is on a vertex, it should be obvious that the path will just be the path of the perimeter of the triangle since there can only be one parallel line through a point not on a line.
When P1 is a midpoint of one of the sides, it will take only 3 lengths to get back to P1. Furthermore, the length of the path will be equal to the perimeter of the medial triangle.
Return to Final Assignment page.