Assignment 10

Just as we can have parametric curves in the plane, we can have them in threespace by having a trio of functions x = f(t), y=g(t), and z = h(t). For convenience, I will use the notation (f(t), g(t), h(t)) from now on.

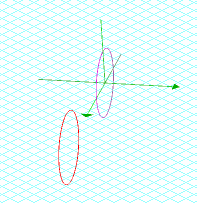
For example, (cos t, 0, sin t) would be a circle on the y = 0 plane, and (4 + cos t, 0, sin t) would be the same circle shifted to the right along the x-axis by four units. The graphs of these two functions follows:

We can shift this circle out of the y = 0 plane and into the y = n plane by graphing (4 + cos t, n, sin t). This is shown for several values of n in the following graph:

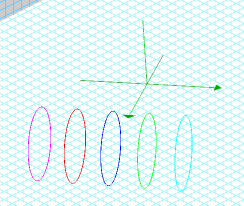
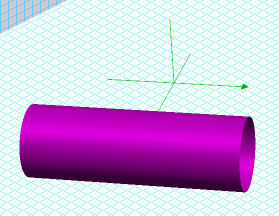
After viewing the above graph, it should be apparent that if we could simultaneously graph all functions of the form (4+cos t, n, sin t), with n being any real number, then the resulting graph would be a cylinder. This can be done by introducing a second parameter u, giving us (4 + cos t, u, sin t). To graph parametric equations with two parameters in Graphing Calculator, the parameters must be u and v, so to graph the cylinder, we must change the t to v, getting:

We can create a more interesting surface as follows:

Rather than shift the circle (4 + cos t, 0, sin t) into different planes parallel to y = 0 (as we did to make the cylinder), we could spin the circle around the z-axis. If we fix t above, we get a point, and the radius of the circle created when we spin this point around the x-axis would be 4 + cos t. Since a circle of radius a using parameter v is given by (a cos v, a sin v), our circle for a fixed t would be ( (4 + cos t) cos v, (4 + cos t) sin v, sin t ), and as t varies, we get a torus, which we can graph in Graphing Calculator by changing the t's to u's:

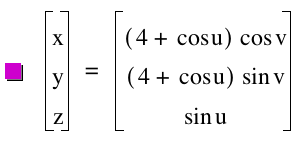
Graphs for fixed values of u and fixed values of v give more insight into how the parametric equations for a torus define the torus:

for fixed values of u:

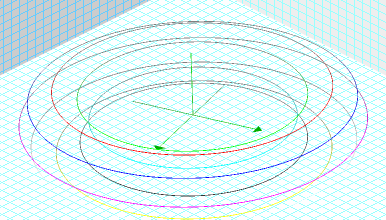
for fixed values of v:

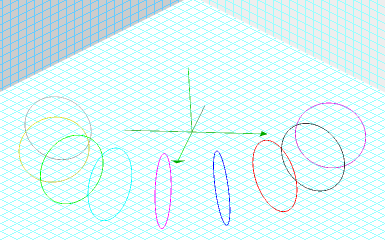
You might be surprised to know that these two families of circles do not contain all circles that lie on the torus! Another family of circles, those formed by the intersection of planes tangent to the torus at exactly two point exists: