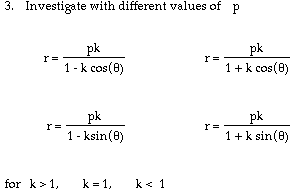
Assignment 11

For this assignment, I chose to write up problem number three:

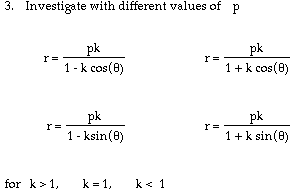
Note: The parameter k is called the "eccentricity" of these conics. It is usually called "e" but for many software programs e is a constant and can not be set as a variable.

After experimenting with the graphs of these equations with different values of k and p for a while, I developed the following conjectures:

• When |k| > 1, the graph of the equation is a hyperbola
• When |k| = 1, the graph of the equation is a parabola
• When |k| < 1, the graph of the equation is an ellipse
• The graph when k=a is the same as the graph when k=-a

The following three tables outlines some other patterns that I noticed while experimenting with graphs of these equations. There is one table for each conic section:

When |k| > 1

When |k| = 1 (parabola)

When |k| < 1 (ellipse)