.Assignment 3
I chose to write up investigation #1:
We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b = 2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersets the x-axis twice to show two negative real roots for each b.
Now consider the locus of the vertices of the set of parabolas graphed
from .
Show that the locus is the parabola 
. Generalize.
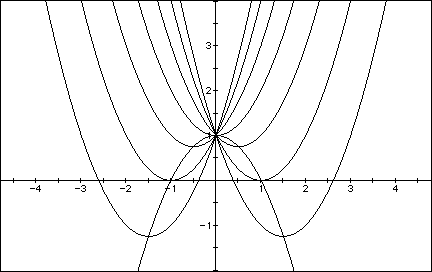
The vertices of 
are the points where 
.
Thus, b = -2x, and so
.
I modeled this situation on Geometor's Sketchpad using similar triangles and GSP's locus function:
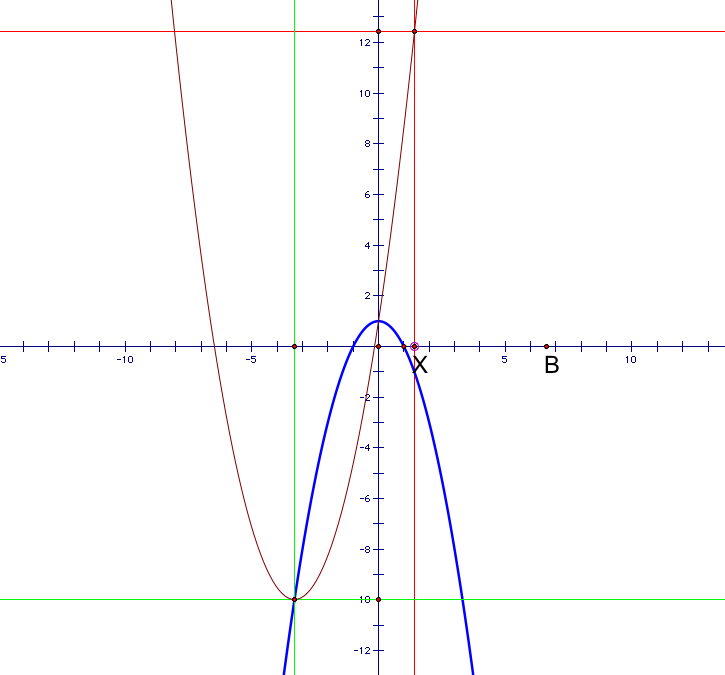
By downloading the file here and sliding the points B and X, you might figure out how I created this sketch.
In general, if 
,
the vertices are the points where 
.
Thus b = -2ax, and so 