Assignment 6
1. Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.
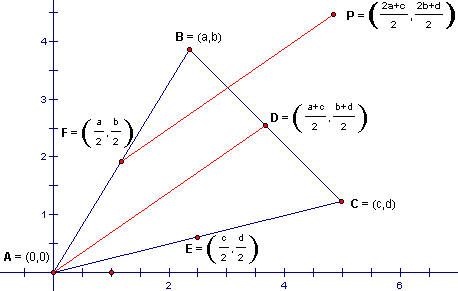
Given any triangle, we can place one vertex on the origin, and give the other two vertices arbitrary coordinates, as shown in the diagram below. Using the midpoint formula, we can also assign coordinates to the midpoints, D, E, and F, of the triangle edges. If we translate the point F by the vector going from A to D, it's image P will have the coordinates labeled below:
Similarly, if we translate the point C by the vector going from E to F, it's image Q will have the coordinates labeled below:
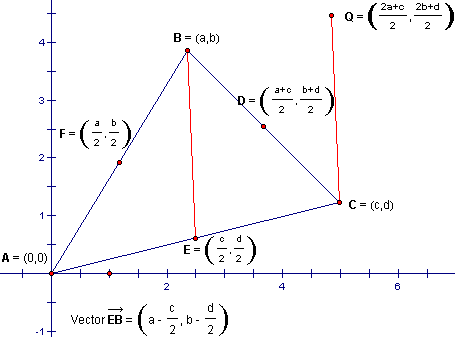
Notice that P = Q, which means that triangle FPC is a triangle with sides congruent to triangle ABC's medians. (Because FP is congruent to AD, PC is congruent to BE, and of course, FC is congruent to itself.) We therefore have a simple construction of the required triangle.
I modeled this situation using this GSP file. After some experimentation, I made the following conjecture:
The area of the median triangle is three-fourths the area of the original triangle.
My proof of this fact follows.
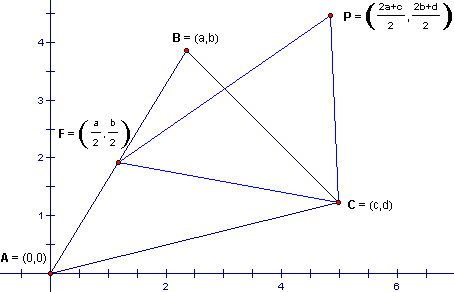
The original triangle ABC, and the second triangle FPC, with its three sides having the the lengths of the three medians of ABC, are labeled below:
We learned in Linear Algebra that the area of a triangle with
coordinates (a,b), (c,d), and (e,f)
is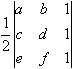 
, so the area
of ABC is 
,
and the area of FPC is 
,
thus area(FPC) = 3/4 * area(ABC).