Assignment 8
I chose to write up investigation #15:
Find the triangle of minimal perimeter that can be inscribed in a given triangle. (For a start, you may want to restrict your investigation to the given triangle being acute.)
I began this problem by working a similar, simpler problem:
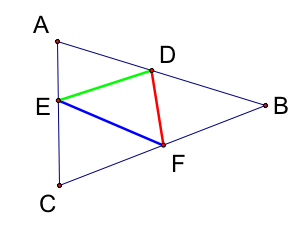
Suppose the triangle ABC has an inscribed triangle DEF with D fixed along AB. How can we pick E along AC and F along BC so that the perimeter of triangle DEF is minimized?

If we reflect along the line BC we get a new triangle and inscribed triangle:
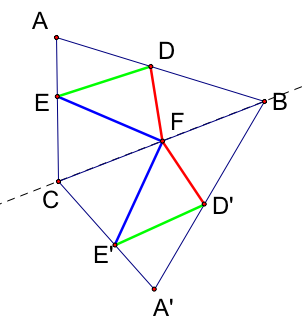
If we reflect these two new triangles along the line CA', we get:
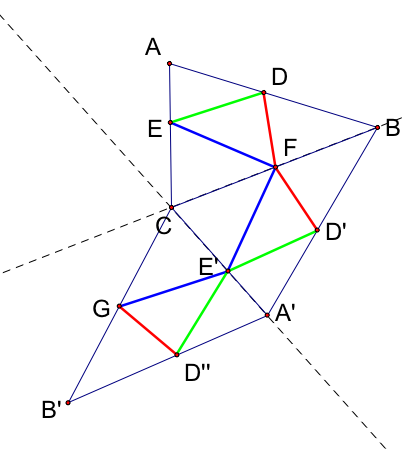
Notice that the perimeter of our inscribed triangle is equal to the length of the path DFE'D''. How can we move E and F so that this length is minimized? So that the path lines up with the line DD'':
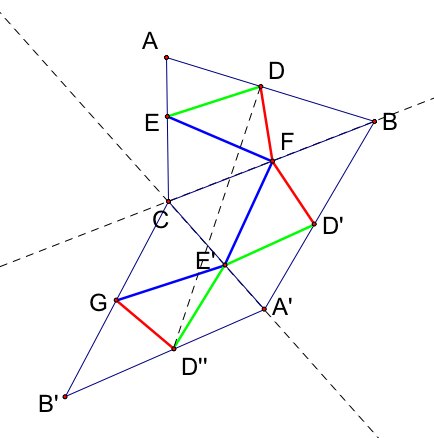
To solve the original problem, we must find where D should be along AB. We now know that this would be the point that minimizes the segment DD'' in the diagram above. Since the triangles are constructed from reflections, we know that CD and CD'' are congruent, thus the triangle D''CD is isosceles.We can thus minimize the length of DD'' by minimizing the length of CD. Since CD is minimized when D is on the line perpendicular to AB and through C, D is on the altitude through AB.
If we fix D on the altitude through AB, then using the above algorithm for minimizing the perimeter of the inscribed triangle, we will find that E is on the altitute through AC, and F is on the altitude for BC.
Note that if our triangle is obtuse, only one altitude intersects the triangle. One point of the inscribed triangle will be at this interesection. The perimeter of the minimal triangle will thus approach the length of this altitude as the other two vertices on our inscribed triangle get closer to vertex of the original triangle that intersects this altitude.