Assignment 8

For this assignment, I chose to write up problem number nine:

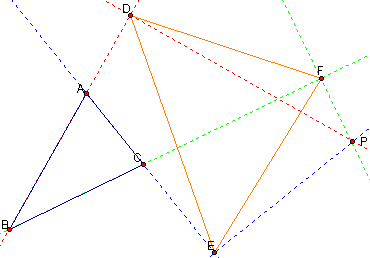
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle). This line segment is called the Simson Line.

This picture shows pedal triangle DEF to triangle ABC for pedal point P. This GSP file contains a script tool for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC. I used this script tool and discovered several places (the green points) where I could place P so that the pedal triangle would be degenerate:

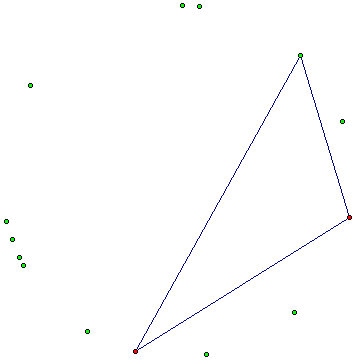
These points appear to lie on the circumcircle of the triangle. The following theorem is indeed true: P lies on the circumcircle of ABC if and only if the pedal triangle DEF to triangle ABC of point P is degenerate. After failing numerous attempts to prove this fact, I could not resist peaking at this proof. I had more success at proving the following MUCH simpler facts:

The pedal triangle to triangle ABC of point P, when P is the incenter of ABC has vertices DEF, which are the points on triangle ABC tangent to the incircle.

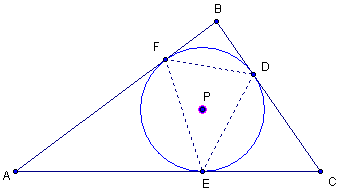
By definiton of pedal triangle, PF is perpendicular to BA, PD is perpendicular to BC, and PE is perpendicular to AC.

The pedal triangle to the triangle ABC of point P, when P is the orthocenter of ABC is the medial triangle of ABC.

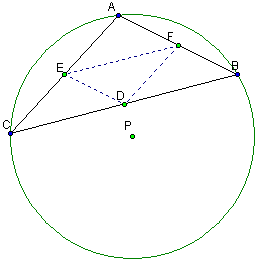
By definition of orthocenter, the line through P and F is the perpendicular bisector of AB, the line through P and D is the perpendicular bisector of BC, and the line through P and E is the perpendicular bisector of AC.