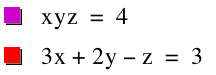
Part B: Multiple Solutions

1. Find as many solutions as possible for A, B, and C that satisfy both equations:

ABC = 4

3A + 2B - C = 3.

What observations can you make about your results? Again, we discussed some approaches to this one in class. Your task is to prepare a write-up that explores this task. (Not required, but you might want to consider how to explore this one with a spreadsheet as well as with graphing tools.).

2. Create another set of equations that also yield a useful exploration.

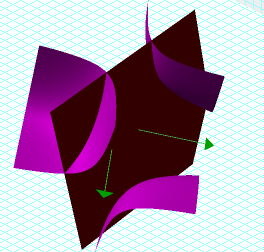
I began this problem by graphing the two equations using Graphing Calculator. The graph is shown from two angles:

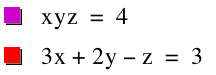By solving for z in the equation for the plane, and substituting this value in for z in the first equation, we get a graph that shows us the possible values of x and y. By picking (x,y)-coordinate pair on this graph, we can plug it in to get z. Giving us a solution to the equation. The solution set to this system of equations results from finding z for all such (x,y)-coordinate pairs. This graph gives us an idea of what x and y values will satisfy this system of equations:

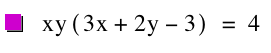
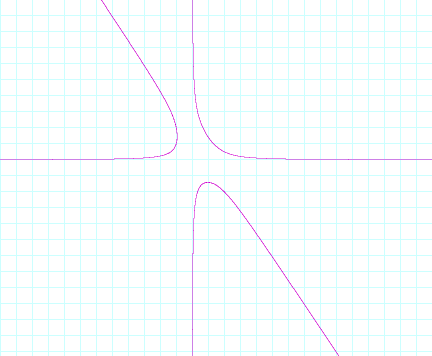
When we expand the above equation, we notice that it is a quadratic in x:

, so

Using the quadratic formula (or Maple ;) ), we find that:

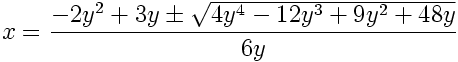
We can now parametrize our solution set, where t ranges over all real numbers by:

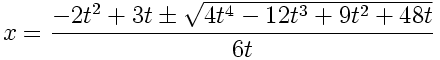
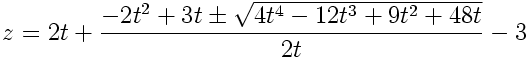
Another exploration could be to solve the following system of equations:

The graph of these two equations follows. With the addition of one more sphere, these equations could be useful explaining how triangulation and GPS work.