Assignment 12 Write-up
4. Generate a Fibonnaci sequence in the first column using f(0) = 1, f(1) = 1, and
f(n) = f(n-1) + f(n-2)
a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. What happens as n increases? What about the ratio of every second term? etc.
b. Explore sequences where f(0) and f(1) are some arbitrary integers other than 1. If f(0)=1 and f(1) = 3, then your sequence is a Lucas Sequence. All such sequences, however, have the same limit of the ratio of successive terms.
First of all, let's show the table:
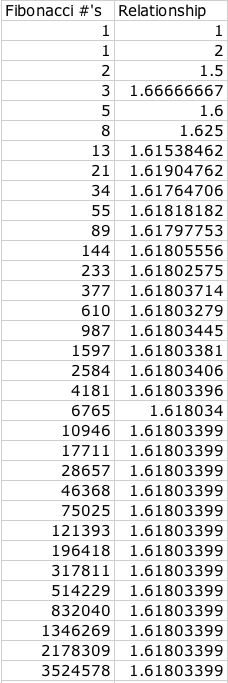One
can see that as n increases, the sequence approaches infinity.
Another interesting fact to see is that the relationship between
f(n) and f(n-1) approaches a "mysterious" number--1.618.
. .
This number is none other than the number "phi" and is also known as the Golden Ratio!! This number is found all throughout nature--nautilus shells, pine cones, sunflowers, and even the human body. For even more information on this wonderful number and the Fibonacci sequence, click here. (I think that showing real life examples of the Golden Ratio to students would be very beneficial to this lesson.)
Now let's look at a sequence where the first two numbers are arbitrary.
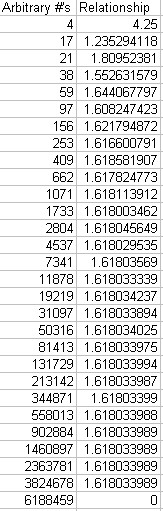This
sequence also goes to infinity and the Golden Ratio is present here as well! This means that the formula derived in the link above applies to all sequences
that begin in this manner.