Assignment 8 Write-up
12. Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove:
1.
2.
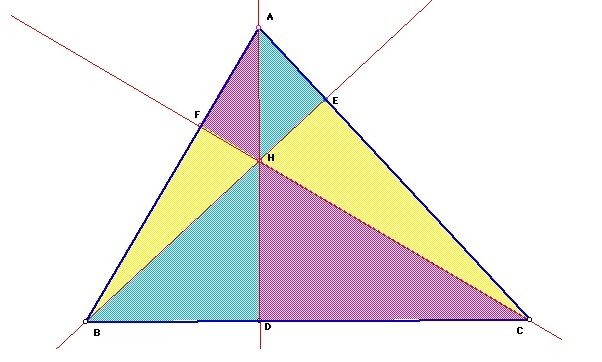At
first, I thought that I could prove this by showing proportions, such as HD =
2HA. However, after calculating these lengths I realized that this was not
true. (I must have been thinking about properties dealing with medians and
centroids.) Then I realized that I'm dealing with a whole lot of
triangles, so what better way to prove this than by using a lot of properties of
triangles? First, let's remember that the area of a triangle =
.5(base)(height). Now, to get started. . .
Now, to prove the second equation. . .
The first thing to notice is that AD = AH + HD, BE = BH + HE, and CF = CH + HF. Now, with a little switching and substituting, we get
This can be rewritten as
Remember that we have proven that
So it basically comes down to 3 – 1 = 2.