Here is the given data on the price of stamps.
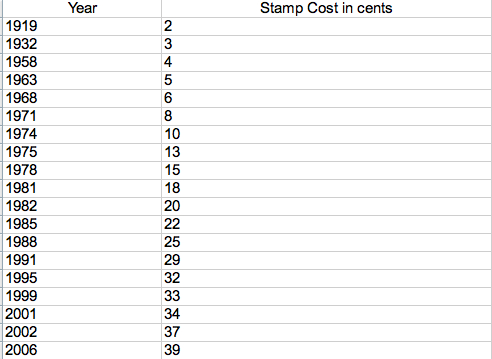
And here is a chart of it.
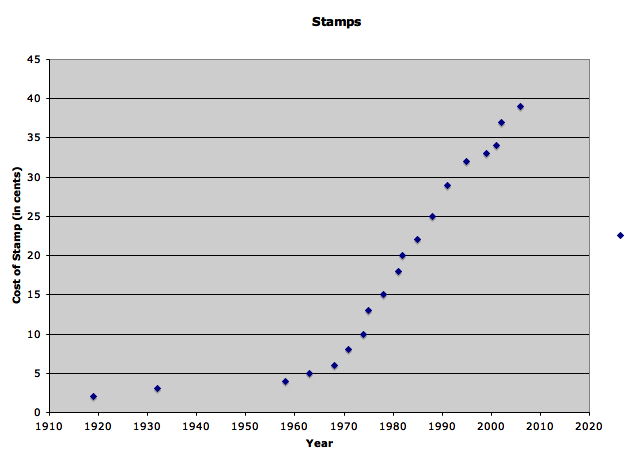
In order to answer the first question--how long it will be before a stamp costs $1.00--we need to find an equation that matches our given data. If you'll notice, the above chart looks a lot like an exponential equation. So let's try one of those!
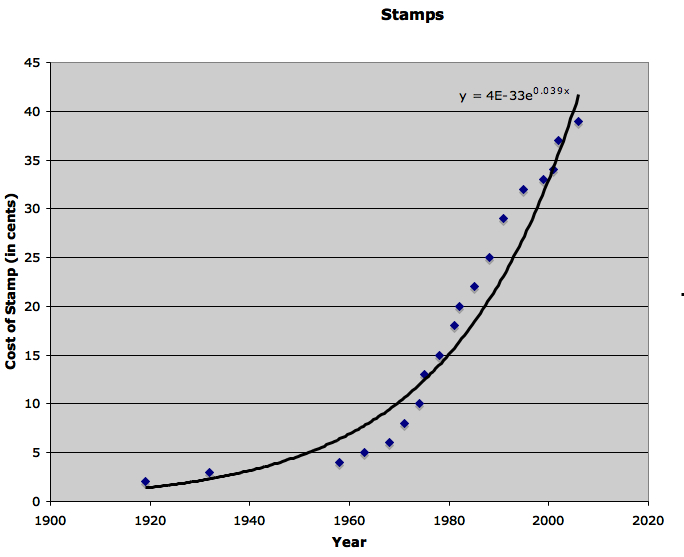Well, it looks like
the best equation is an exponential one. Now, in order for us
to find out how long it will be before a stamp costs $1.00, all
we have to do is plug in 100 for our y-value (since y is in cents)
and see what number comes up for x! (Remember that this is only
an approximation. As you can see from the chart, this is not a
dead-on, accurate equation.)
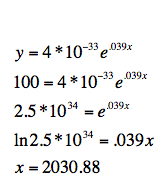So, according to
our data, a stamp should cost $1.00 around the year 2030.
To get the answer to the next question, does repeat the process all over again with 74 instead of 100 = y.
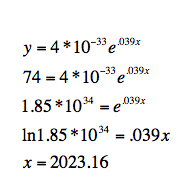So the price of
a stamp should be double what it is right now somewhere around
2023.
It's hard to tell when the next increase will be simply because we don't know how much that increase will be. If it is a one cent increase, then expect that to occur in 2007 (just plug in the numbers into the equation). If it's a two cent increase, then that may take place somewhere around the year 2008. Who knows?
According to our data, the price of a stamp will double in about 16 years. This is pretty far off from the prediction that it would double every 10 years. This leads me to believe that it's hard to tell just what is a good model for the cost of stamps. If we only had the data that was available prior to 1975, we would have a completely different graph and equation. In 1975, no one could have predicted the price of stamps in 1990. And in 1990, no one could have predicted the price of stamps today. Who can say that we have the most accurate equation right now? Perhaps 10 years from now our graph will look completely different than what is imagined.