From Barns to Satellites...

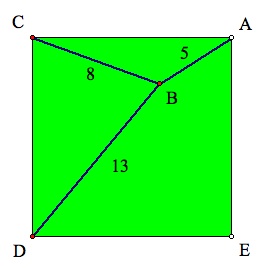
This problem asks to find the location of a point, the barn, that has fixed distances from three different points, the corners of the field, where all points are located on a plane. By understanding the geometry involved in this problem, it is also possible to understand how electronic global-positioning equipment works.

Using Circles to Find a Location

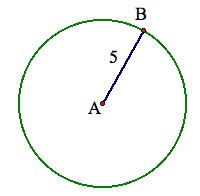
Since we are dealing with fixed distances from points, circles are going to play a key role in pinpointing the location of the barn. When one of the distances, such as the barn is 5 miles from point A, is provided, the location of the barn is narrowed down to being one of the points on a circle centered at A with a radius of 5 miles. While this would certainly makes the barn easier to search for, it is by no means a precise description of its location.

By including a second fixed distance to describe the location of the barn, two circles can now be used. In this case, we will include the barn's distance from C, 8 miles. The inclusion of this second circle will narrow the location of B to at most two points, the intersection points (or point, if A, B, and C are collinear) of the two circles.

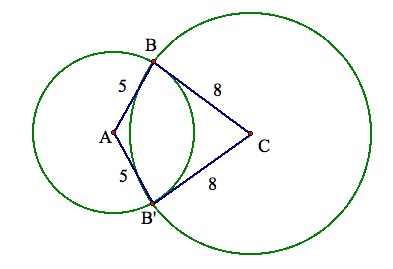
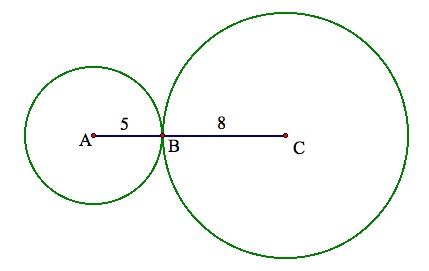
While the degree of uncertainty with two distances is minimal, an accurate location of B is attained by adding a third distance. Staying within the context of the problem, the distance from the barn to point D, 13 miles, is incorparated into the model. Provided that A, C, and D are noncollinear, this addition ensures that B will only have one location.

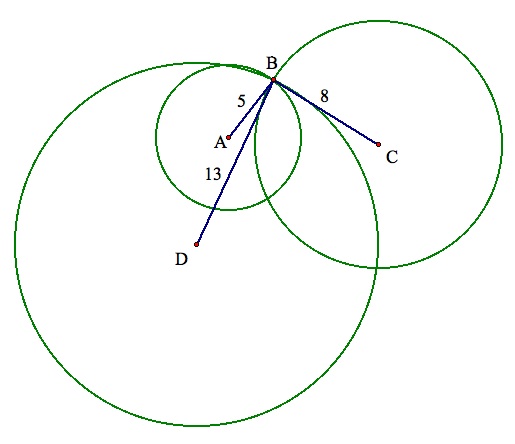
Why can one be certain of only one intersection of all three circles? An algebraic analysis can shed some light on this question.

Trilateration

The process of trilateration finds the location of a point that is described in terms of fixed distances to three known points. In order for this process to be executed with minimal computation, the three known points must be oriented such that one point represents the origin (0, 0) and one point represents a point on the x-axis (p, 0). The third point (q, r) will be realigned according to its relative position to the first two. One way to perform this transformation is to use polar coordinates. Once the three points are oriented in the manner described above, three equations are used to describe the location of the point in question, with the distances to the known points represented by d.

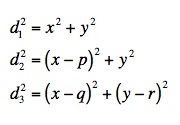
By subtracting the second equation from the first, x is attained. Substituting this value back into the first equation will result in values for y.

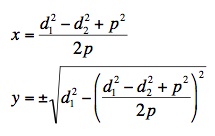
To determine which value of y correctly describes the point in question, x and y are substituted into the third equation. Try practicing this technique with the following example:

P is located 13 units from (0, 0)

P is located 5 units from (9, 15)

P is located 20 units from (21, 0)

From this information, you should have determined that the coordinates of P are (5, 12). It is important to note, if the points were reoriented prior to obtaining a solution, the coordinates of the solution must be reverted back to the original orientation. To deal with situations like this, I created an Excel spreadsheet to perform the calculations. To download it, Click Here.

The Location(s?) of the Barn

While the trilateration method is helpful in understanding how the location of a point can be determined, it cannot solve the barn problem introduced above. As the dimensions of the square field are unknown, it is impossible to determine the coordinates of the three reference points. The analysis of the problem can be continued, however, by using Graphing Calculator or Geometer's Sketchpad. By letting the lower-lefthand corner of the field have coordinates (0, 0) and the length of the field be n, the coordinates for the other corners of the field are (0, n), (n, n), and (n, 0). From these points, a system of equations similar to the one described above is set up and graphed.

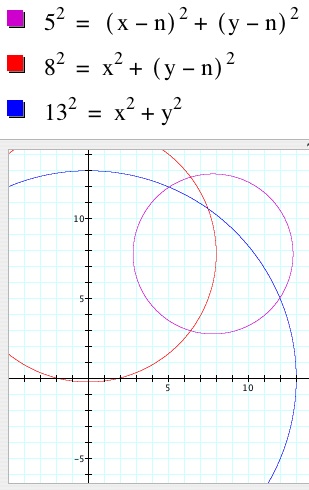
This graph represents n = 7.8. As all three circles do not intersect at any point on the graph, it can be concluded that no solution exists for a field with length of 7.8 miles. By varying the value of n, the circles will move across the plane The three circles intersect at one point in two different places, when n = 6.41(below left) and n = 12.35 (below right). It is interesting to note that, in the first case, the barn is located outside the field. To download this Graphing Calculator file and animate the graph, Click Here. To download a similar sketch made with Geometer's Sketchpad, Click Here.

............

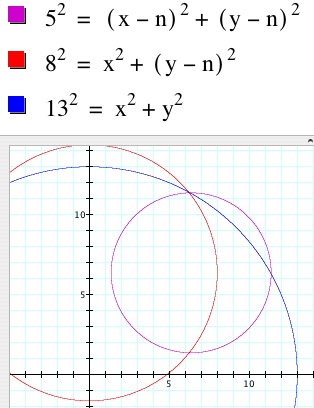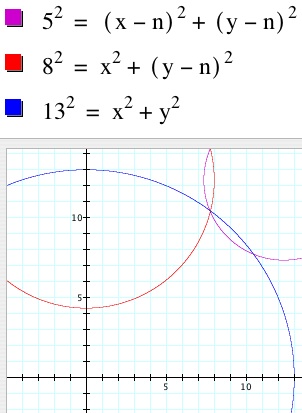
So, to answer the question regarding the barn's location. If the field has a length of approximately 6.41 miles, the barn is located outside of the field and is 4.99 miles from the nearest road. If the field has an approximate length of 12.35 miles, then the barn is located in the interior of the field and is 1.92 miles from the nearest road.

Global Positioning Systems

Global positioning technology is now found in many devices such as cars, watches, cell phones, and satellite dishes. A global positioning system (GPS) operates by receiving signals from satellites positioned around the earth. From these satellites, a GPS receives broadcasted information about the each satellite's position and the time at which the information was broadcasted. Using this information, the GPS receiver calculates the distance to the satellite and then its own location. Due to the fact that the earth is rotating and moving along its orbit and that the satellites are moving themselves, this is a very complicated process. The basic premise behind these calculations, however, is trilateration expanded to three dimensions.

In two dimensions, three circles were needed to locate the position of most points. For three-dimensional calculations, this notion will be expanded in two ways. First, spheres will be used instead of circles. Second, four spheres will be needed to ensure the location will be accurate. Look at the graph below, showing three intersecting spheres.

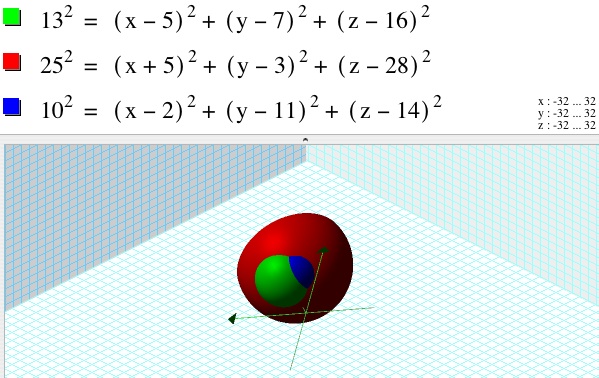
Notice that there are two points that all three spheres share. It is for this reason that a fourth sphere is required for accurate calculations. In the context of GPS, the receiver must receive a signal from at least four different satellites in order to correctly calculate its location.

The calculation method, as mentioned above, is similar to two-dimensional triangulation. Again, the four points from which the distances are known must be reoriented. In this case, one point will be the origin (0, 0, 0), one point will lie on the x-axis (p, 0, 0), and one will lie on the xy-plane (q, r, 0). The fourth point will have an arbitrary location (s, t, u). This results in the following system of equations:

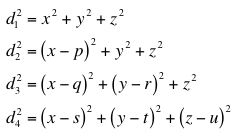
A method similar to the two-dimensional method shown above yields the following solutions:

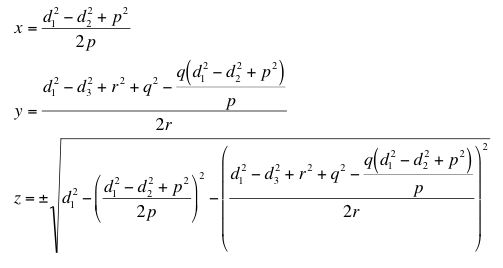
Once again, substituting these values into the final equation will determine which point is the correct solution. Can you create a set of points and distances that can be used to locate a point in three dimensions?

More information about global postitioning systems is available online. Some links to websites that I found particularly interesting are available below.

How Stuff Works: Global Positioning Systems

Trimble: GPS Tutorial (Macromedia Shockwave required)

University of Colorado: The Geographer's Craft

Wikipedia: Global Positioning Systems

Leland West: The GPS Device (Suggested by Mrs. Burns's class at Monument Charter School)