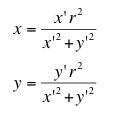
Recall from the introduction, x and y can be stated in the following manner:
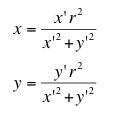
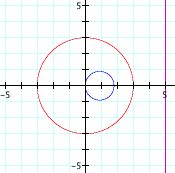
Once we know how to express the coordinates of a point in terms of the coordinates of its inverse with respect to gamma and the radius of gamma, it becomes possible to examine the inverses of curves. Consider, for example, the line whose equation is x = 5 and gamma is centered at the origin with radius 3.
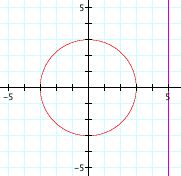
Can you make a conjecture about the inverse of the line? The equation for the inverse of this line with respect to gamma can be found by making the proper substitution for x.
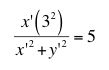
Using algebraic techniques, including completing the square, this equation can be transformed into the standard form of a circle. Does this confirm your conjecture?
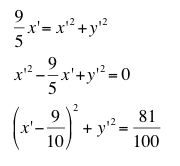 ...
...
On the Geometric Inversion Homepage are links to some more challenging transformations and their solutions, with graphs. A wide array of exercises of this nature can be developed, depending upon the tenacity of your students. If you choose to create your own exercises, note that it is much easier when you choose a gamma that is centered at the origin.