Geometric Inversion: A Conceptual Foundation

Geometric inversion is means of a transforming points in a plane with respect to an arbitrary circle, called the circle of inversion. For the purposes of this unit on geometric inversion, the circle of inversion shall be called gamma and have center O and radius r. Geometric inversion transforms each point P in the plane with into a point P', also in the plane, such that O, P, and P' are collinear and the following relationship is true:

(OP)(OP') = r²

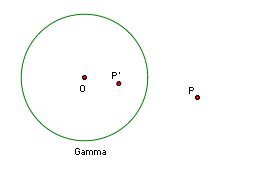
The figure below depicts P and P' with respect to gamma.

To download a Geometer's Sketchpad sketch with this figure, Click Here. Using this sketch, explore the model by changing the position of P.

1. What if P is located in the interior of gamma?

2. What if P is on gamma?

3.Where is the inverse point of O?

4. Can you verify the conjectures you made in questions 1, 2, and 3 using the relationship between OP, OP', and r?

P and P' will maintain a relationship where one is partitioned outside gamma and one is inside. When P is in the interior of gamma, OP < r. Thus OP' > r for the relationship between the three distances to hold. When P is on gamma, OP = r. Thus, OP' = r as well. O has no inverse point. If P were located at O, then OP = 0. This quantity, when substituted in the relationship causes OP' to be undefined. A good way to discuss this case is to move P close to O and examine the change in OP and OP'.

To continue with the introduction by examining the analytic geometry of geometric inversion, Click Here.

To return to the Geometric Inversion homepage, Click Here.