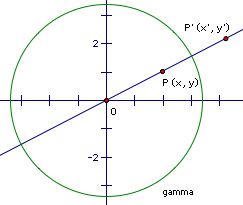
Inverses of Points
Consider the case where the circle gamma is centered at the origin with radius r. Let P and P' have the coordinates (x, y) and (x', y'), respectively.

We know that, since P and P' are inverse points with respect to gamma, (OP)(OP') = r2. Using the coordinates of P and P', this relationship can be reexpressed as:
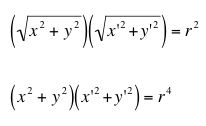
1. Find (x', y'), the coordinates of P', in terms of x and y.
2. How would you modify the above equations and the coordinates you found in question 1 so that the center of gamma is at a point other than the origin?
Similar triangles can be formed by dropping perpendiculars from P and P' to the x-axis, creating the proportion below.
Substituting the value of x' 2 from the equation above,
By factoring and simplifying, the value for y' is found with respect to x, y, and r. By a similar process, x' is also found:
Note that equations for x and y with respect to x', y', and r will be similar in structure.
When gamma is not centered at the origin, let the center of gamma be (h, k). The equations for x' and y' are: