The concept of geometric inversion can be applied to three-dimensional space as well. The process of stereographic projection maps the points of a sphere onto a plane in a one-to-one correspondence. One area where this kind of procedure would prove helpful in in geography, where a mapping of a three-dimesional surface (the globe) to a two-dimesional surface (a map) is often performed. To begin to imagine this process, start with a sphere that is resting on a plane.

Below is a cross-sectional representation of the picture above. In this diagram, S represents the point where the sphere is tangent to the plane while N is the point on the sphere opposite S. Another way to think of these points is in terms of a planet. If the point of contact with the plane is the south pole (S) of the planet, N would be the north pole.
To map a point P on the sphere to a point P' on the plane, a line is constructed through that point and N. The point where this line intersects the plane is P'.
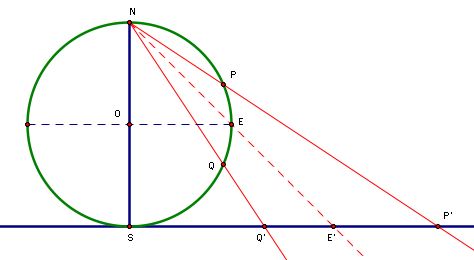
1. In the above diagram, Q is the reflection of P over the segment OE (the equator). Is there a constant relationship between SP' and SQ'?
2. Where is the north pole, N, mapped?
3. Does the image of the entire sphere fill up the plane?
4. What is the image of the equator?
5. Where are points in the southern hemisphere mapped? The northern hemisphere?
The Geometer's Sketchpad file from which the above diagram was taken can be accessed from the Geometric Inversion homepage. 1) The relationship between SP' and SQ' is (SP')(SQ')=SE2. A proof of this relationship is in the GSP file. 2) The north pole is not mapped to the plane, as no line can be constructed with only one point. 3) Yes. 4) A circle with center S and radius 2OE. 5) The southern hemisphere is mapped to points inside the image of the equator. The northern hemisphere is mapped to points outside of the image of the equator.