The Task: Construct the graphs for a quadratic equation in standard form where two of the values for a, b, and c are fixed. Interpret the graphs.
The standard from of a quadratic function is:
For this investigation focuses on fixing the values of a and c while varying the value for b. As a beginning, the value of a and c are assigned an arbitrary value of 1. A set of functions with values of b ranging from -5 to 5 is presented below.
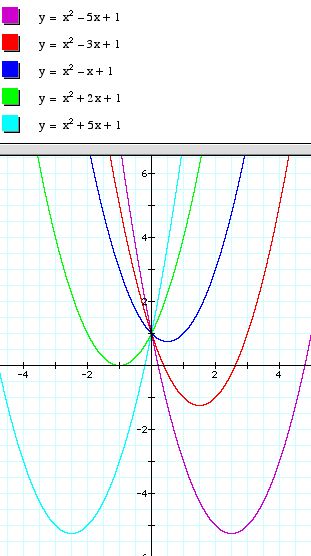
One interesting aspect of this graph is the location of the vertex for each parabola and how this location changes as b changes. While it may be difficult to grasp this relationship from the graph above, it is easily seen by viewing an animated graph.
Click here to see the Animated Graph. (Your computer must have Graphing Calculator software to exercise this option.)
As b changes, the vertex of the parabola appears to move along a parabolic path. This can be confirmed algebraically.
For the quadratic function,
the vertex has the coordinates
Substituting the value x for 
gives us the coordinates 
. Thus, the locus
of the vertices for these quadratic functions is
Inserting the graph of v into the graph above confirms that the vertex of each parabola lies on v.
Click here to see the Animated Graph tracing the function v.
What happens when the values of a and c are changed? Using the same algebraic derivation from above will result in a more general form of the function v.
Theorem: Let a family of parabolas
be of the form 
, where a and c are fixed values and b
is any real number. The locus of points formed by the vertices
of the graphs in this family is a parabola defined by the function
Can you derive this function? Click here
to see the Derivation
of the General Form.