

The Medial Triangle
For any given Triangle ABC, its medial triangle is constructed by finding the midpoints of its three sides (Segments AB, BC, and AC) and constructing segments to join these midpoints. In the figure below, Triangle DEF is the medial triangle of Triangle ABC.
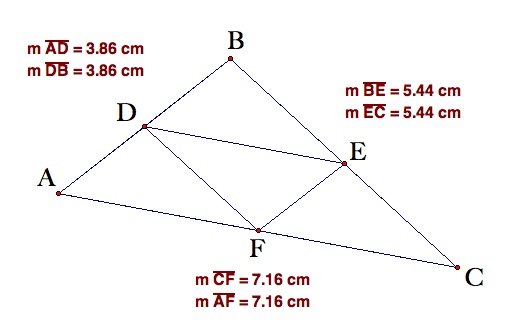
An important property of the medial triangle is that it divides the original triangle into four smaller, congruent triangles that are each similar to the original triangle. Thus Triangles AFD, DEB, FCE, and EDF are congrent to each other and similar to Triangle ACB.
Can you prove this conjecture ?(You may find the triangle midsegment theorem helpful)
What is the ratio of the corresponding side lengths between triangle ACB and the smaller triangles?
The examination of the triangle centers of any triangle and its medial triangle reveals some interesting relationships. For a quick review of the four triangle centers, Click Here. Below are some conjectures regarding the centers of medial triangles.
Conjecture #1: The centroid of a triangle is also the centroid of its medial triangle.
To begin considering this hypothesis, examine the figure below.
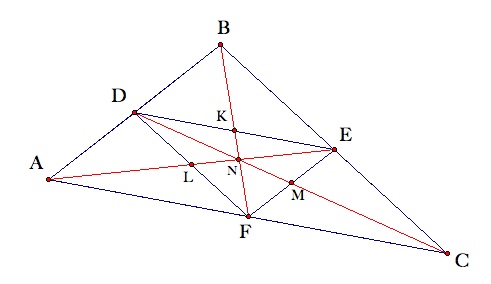
It certainly appears that this is the case. Since appearances can often be deceiving in geometry, a proof of this conjecture is offered below.
Given: Triangle DEF is the medial triangle of Triangle ABC; N is the centroid of Triangle ABC.
Prove: N is the centroid of Triangle DEF.
If N is the centroid of Triangle DEF, then Segements EL, DM, and FK are medians of Triangle DEF. If this is the case, then K, L, and M must be the midpoints of Segments DE, DF, and EF, respectively. By verifying each of these midpoints, the proof will be complete.
In order for L to be the midpoint of Segement DF, Segements DL and LF must be congruent. One way to verify this congruence is by looking at Triangles ALF and ELD.
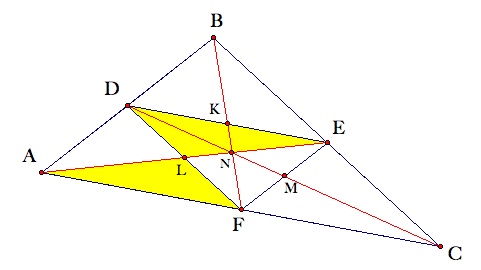
(1) Angle ALF is congruent to Angle ELD because they are verticle angles.
(2) Since D and E are midpoints of Segments AB and BC, respectively, Segment DE is a midsegment of Triangle ABC. Therefore, the length of Segment DE is half the length of Segment AC. Since F is the midpoint of Segment AC, Segment AF is half the length of Segment AC. Therefore, Segements AF and DE must be congruent.
(3) The four smaller triangles formed by the construction of a medial triangle are each similar to the original triangle. Thus Angles LFA and LDE are congruent as they are corresponding parts of similar triangles.
From (1), (2), and (3), Triangles ALF and ELD are congruent by Angle-Angle-Side. Thus, Segments DL and LF are congruent (since corresponding parts of congruent triangles are congruent) and L is the midpoint of Segment DF.
Through a similar technique, it can be
shown that K is the midpoint of Segment DE and M
is the midpoint of Segment EF. Thus, Segments DM,
EL, and FK are medians of Triangle DEF and
N is the centroid. QED : )
Conjecture #2: The circumcenter of a triangle is the orthocenter of the medial triangle.
To begin considering this hypothesis, examine the figures below.
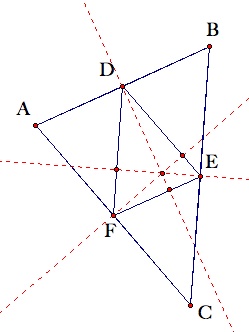
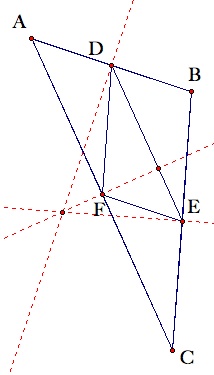
Notice that this conjecture appears to be true for both triangles, even when the point in question lies outside of both triangles. A proof of Conjecture #2 can be found below.
Given: Triangle DEF is the medial triangle of Triangle ABC; Triangle ABC has circumcenter at point M,
Prove: M is the orthocenter of Triangle DEF.
Consider the figure below:
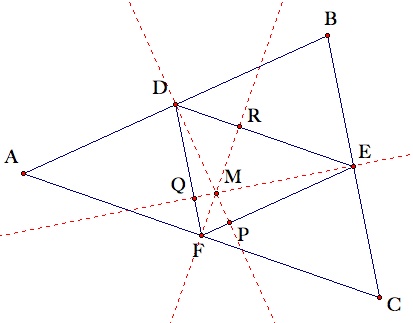
In order for M to be the orthocenter of Triangle DEF, Segements RF, PD, and QE must be altitudes. This means that Lines RF, PD, and QE must be perpendicular to Segments DE, EF, and DF, respectively.
This proof will begin by showing that Line RF is perpendicular to Segment DE. Since M is the circumcenter of Triangle ABC, Line RF is the perpendicular bisector of Segment AC. Since Segment DE is a midsegment of Triangle ABC, it is parallel to Segment AC. If a line m is perpendicular to any segment q, then it must also be perpendicular to any segments parallel to q. Thus Line RF is perpendicular to Segment DE.
Through a similar argument, it can be
shown that Line PD is perpendicular to Segment EF
and Line QE is perpendicular to Segment DF. Thus,
Lines RF, PD, and QE are perpendicular
to the sides of Triangle DEF, making Segments RF,
PD, and QE altitudes and, as a result, M
the orthocenter. QED : )
Further Conjectures
Conjecture #3: The incenter of a triangle, the incenter of its medial triangle and the centroid of the triangles are collinear.
Conjecture #4: From Conjecture #3, the distance from the incenter of the triangle to the centroid is twice the distance from the incenter of its medial triangle to the centroid.
Conjecture #5: The orthocenter of a triangle, the orthocenter of its medial triangle and the centroid of the triangles are collinear.
Conjecture #6: From Conjecture #5, the distance from the orthocenter of the triangle to the centroid is twice the distance from the orthocenter of its medial triangle to the centroid.
Conjecture #7: The circumcenter of a triangle, the circumcenter of its medial triangle and the centroid of the triangles are collinear.
Conjecture #8: From Conjecture #7, the distance from the circumcenter of the triangle to the centroid is twice the distance from the circumcenter of its medial triangle to the centroid.
The proof of these conjectures are left to you. The use of coordinate proofs may be the best approach, as slope and the distance can be expressed in terms of coordinates. Rachael Brown, another doctoral student at UGa, has a page dealing with coordinate proofs and the centers of triangles that may a helpful reference. To view her page, Click Here.